Graph in Data Structures: A Complete Guide with Types, Traversals & Applications

Think of graphs as the invisible architecture that lies beneath many of the systems that we interact with on a daily basis. They are some of the most powerful and adaptable data structures. These explain the connections between individuals in a social network, cities on a map, or web pages on the internet.

Graphs are vital in domains right from logistics and navigation to bioinformatics and artificial intelligence, as they capture complex, many-to-many relationships, compared to simpler structures such as trees or arrays. You can model and solve the issues that reflect the complexity of real-world scenarios by understanding how graphs work.

Key Takeaways:
  • Graphs provide a flexible way to model complex relationships (many-to-many) that go beyond trees or linear structures.
  • Key terminology (vertex/node, edge, path, cycle, directed/undirected, weighted/unweighted) is essential for understanding how graphs work and for selecting the right algorithms.
  • Representation matters: adjacency list is space-efficient for sparse graphs; adjacency matrix gives fast lookups for dense graphs. Choose based on size, operations, and memory constraints.
  • Traversals like BFS and DFS are foundational — they enable solutions to connectivity, cycle detection, pathfinding, and structure discovery.
  • Algorithm choice (e.g., Dijkstra, Bellman-Ford, MST algorithms like Prim/Kruskal, topological sort) depends on the graph’s characteristics (weights, directedness, presence of cycles, etc.).
  • Trees are special kinds of graphs: always connected and acyclic; knowing when a tree suffices vs when a full graph structure is needed can help simplify your design.
  • Always handle edge cases: negative weights, disconnected components, self-loops, and multiple edges. Test with both small and large graphs.
  • Performance & scalability considerations (memory usage, recursive vs iterative implementations, data structure selection) are crucial, especially for large or dynamic graphs.

Let us dive into the intricacies of graph data structures, starting with definitions and key terms, moving on to classification and representation, exploring traversal strategies and algorithms, assessing the complexities, and also the different range of applications. This blog functions as an extensive guide for anyone wishing to understand the fundamentals or improve their algorithmic skills.

Introduction to Graphs in Data Structures

A non-linear data structure called a graph is used to show complex relationships between a group of entities. Graphs are extremely versatile for a range of computational problems because they help us to model many-to-many relationships, in comparison to linear data structures like arrays, linked lists, or stacks.

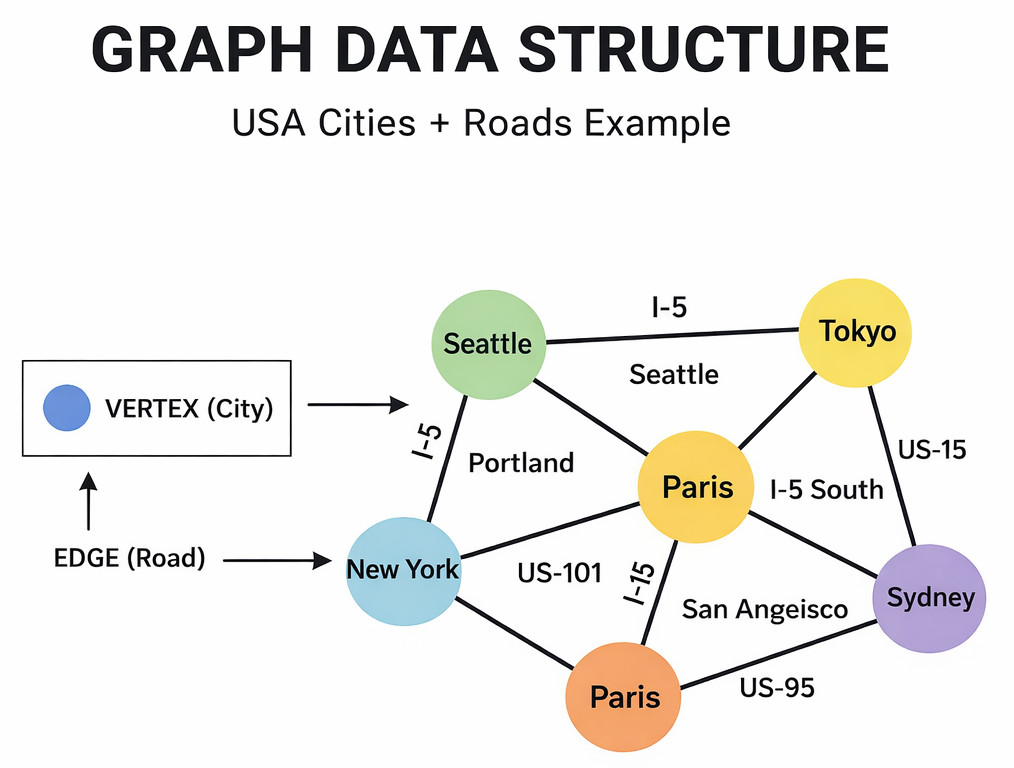
There are two key components that establish graphs:
  • Nodes (vertices): The graph’s entities or objects. Examples include web pages, social network users, and cities on a map.
  • Edge: The connections between vertices are called edges. Examples include hyperlinks between web pages, roads connecting cities, and friendships between people.

A graph can be represented mathematically as G = (V, E), where V and E are finite sets of vertices and edges, respectively.

What Makes Graphs Important?

  • They make it possible to model real-world systems with interdependent entities effectively.
  • From recommendation engines on e-commerce platforms to route planning in GPS systems, they allow real-world applications.
  • They serve as the foundation for numerous algorithms in computer science, operations research, artificial intelligence, and data science.

To put it in simpler terms, understanding graphs gives you the capability to examine and optimize systems where relationships are just as critical as the entities themselves.

Basic Terminology in Graph Data Structures

It is critical to understand the jargon used in graphs before working with them. Algorithms and applications are developed on these terms.

Core Components

  • Vertex (Node): A graph’s basic building block. For example, A user on a social network.
  • Edge: It is a connection that links two vertices. For example, A friendship between users.
  • Adjacent Vertices: Two vertices that are directly connected by an edge.

Properties of Vertices

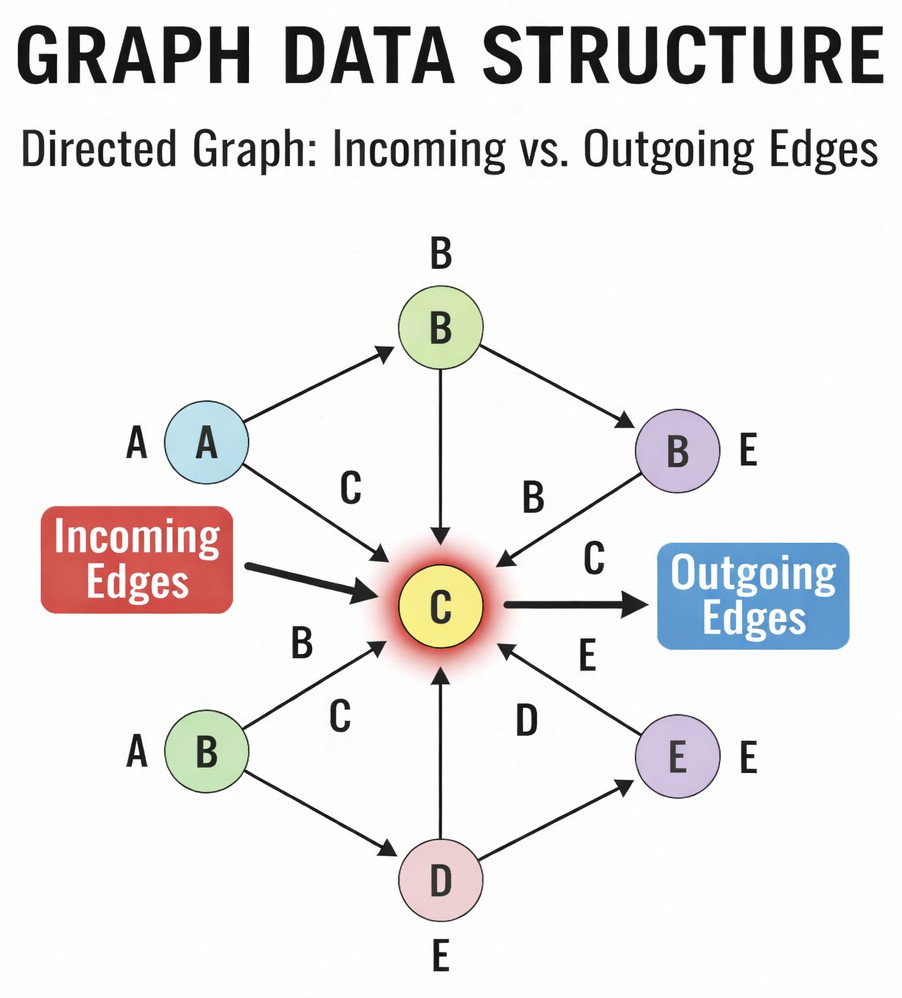
  • Degree of a Vertex: Number of edges connected to the vertex.
    • In-degree: In directed graphs, the number of incoming edges.
    • Out-degree: In directed graphs, the number of outgoing edges.
  • Isolated Vertex: A vertex that has no edges.
  • Pendant Vertex: A vertex connected by only one edge.
  • Path and Connectivity
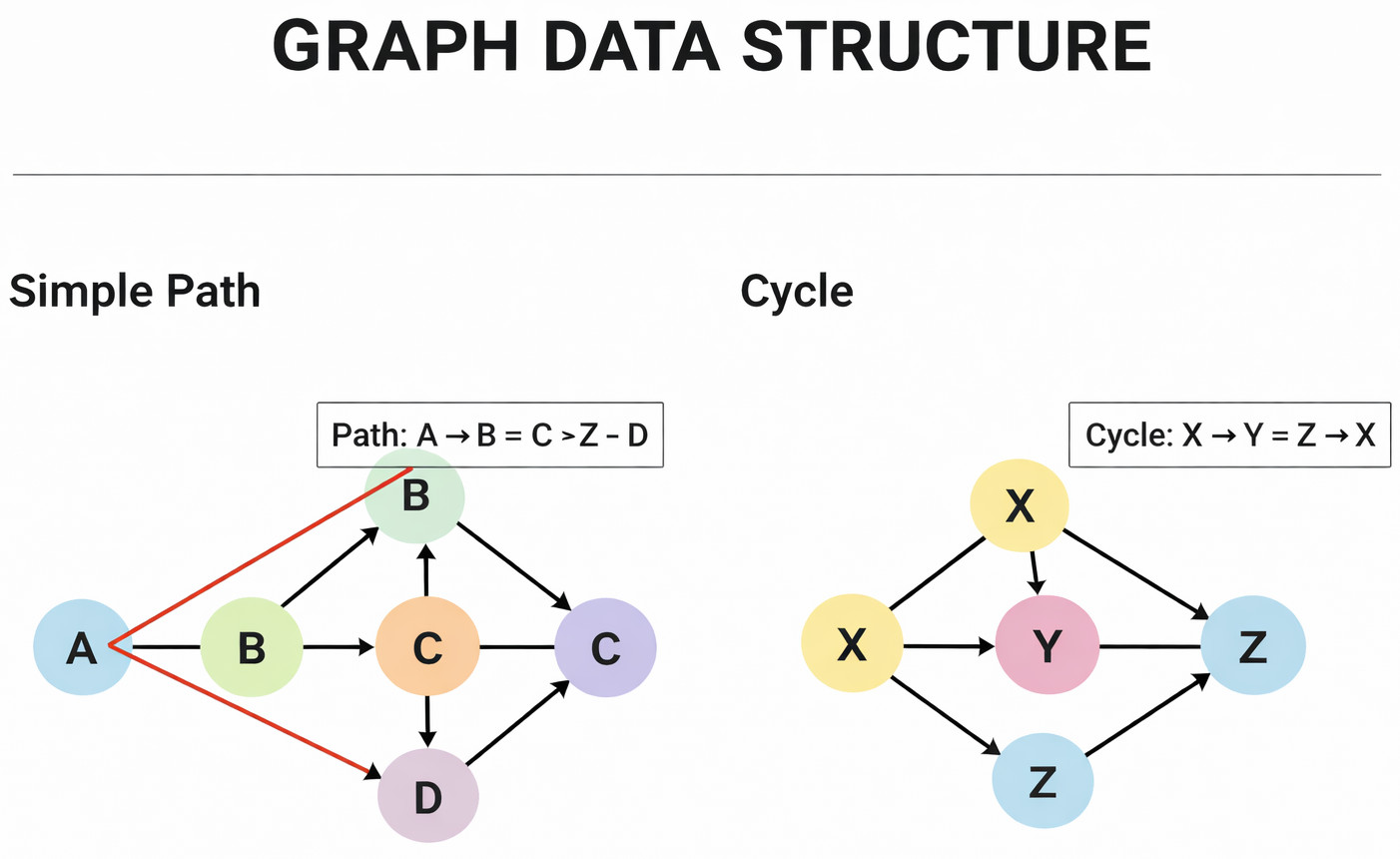
    • Path: An arrangement of edges that joins two vertices.
    • Simple Path: A path that has no repeating vertices.
    • Cycle: It is a path that begins and ends at the same vertex.
  • Connectivity: If a path links each pair of vertices in a graph, then the graph is connected. It is disconnected otherwise.

Graph Classifications

  • Directed Graph (Digraph): One-way relationships are represented by edges with directions.
  • Undirected Graph: Two-way relationships are represented by an edge that has no direction.
  • Weighted Graph: Every edge has a weight, which could be time, cost, or distance.
  • Unweighted Graph: Every edge is considered equal.

It is vital to understand these terms since they have a direct impact on application design, performance, and algorithm selection.

Types of Graphs in DSA

Based on their characteristics, graphs can be segregated into different types:

Directed and Undirected Graphs

  • Directed Graph (Digraph): One-way streets are examples of graphs with edges that have a direction.
  • Undirected Graph: Friendships in social networks are examples of edges that lack direction.

Weighted and Unweighted Graphs

  • Weighted Graph: Each edge has a cost or weight (e.g., distance between cities).
  • Unweighted Graph: All edges are equal.

Simple Graph and Multigraph

  • Simple Graph: Does not have loops or more than one edge.
  • Multigraph: The same vertices may have parallel edges.

Cyclic and Acyclic Graphs

  • Cyclic Graph: Has a minimum of one cycle.
  • Acyclic Graph: Has no cycles.
    • Directed Acyclic Graph: Frequently used in scheduling and dependency resolution, the directed acyclic graph (DAG) is a directed graph devoid of cycles.

Special Types

  • Complete Graph: Each vertex is linked to every other vertex.
  • Null Graph: An edgeless graph.
  • Regular Graph: Every vertex has the same degree.
  • Bipartite Graph: Vertices have edges that only link two sets.

Graph Representation in Data Structures

Performance is determined by how well graphs are represented. Typical techniques include:

Adjacency Matrix

  • A 2D matrix is one in which the presence of an edge between vertices i and j is represented by matrix [i][j].
  • Benefits: Rapid edge lookup and simplicity of implementation.
  • Cons: Inefficient for sparse graphs and needing O(V²) space.

Adjacency List

  • A list of linked vertices is stored in each vertex.
  • Benefits: Needs O(V+E) space and is efficient for sparse graphs.
  • Cons: Edge lookup is slower than an adjacency matrix.

Edge List:

  • It is a list of all edges, each of which is represented by a pair (u, v).
  • Beneficial for particular algorithms (such as Kruskal’s MST).
  • Selecting the representation depends on the types of operations required and whether the graph is sparse or dense.

Operations of Graph

General operations consist of:
  • Vertex Insertion: This adds a new node to the graph.
  • Edge Insertion: Build a new link between two vertices.
  • Vertex/ Edge Deletion: Remove any nodes or connections.
  • Validate Adjacency: Identify if there is an edge linking two vertices.
  • Traversal: Systematically examine nodes (discussed below).

Graph Traversal in Data Structures

In order to examine and process graphs, traversal algorithms are vital.

Breadth-first Search (BFS)

  • Explores neighbors first before shifting to the next level.
  • It makes use of a queue.
  • Applications: It includes web crawlers, shortest path in unweighted graphs, and identifying connected components.

Depth-First Search (DFS)

  • Follow a branch as far as it can go before turning back.
  • Make use of an iterative or repetitive stack.
  • Applications: Includes topological sorting, pathfinding, and cycle detection.

More complicated graph algorithms are based on both DFS and BFS.

Graph Traversal Algorithms

Certain traversal, connectivity, and optimization problems are solved by graph algorithms.

Shortest Path Algorithms

  1. Dijkstra’s Algorithm: Detects shortest paths in weighted graphs with non-negative weights.
  2. Bellman-Ford Algorithm: Works well with negative weights, detects negative cycles.
  3. Floyd-Warshall Algorithm: Identifies shortest paths between all pairs of vertices.
  4. A* Algorithm: Heuristic-based pathfinding, popularly used in AI and gaming.

Minimum Spanning Tree (MST)

  1. Kruskal’s Algorithm: Greedy approach, sorts edges by weight.
  2. Prim’s Algorithm: Expands each vertex individually to build an MST.

Other important algorithms

  1. Topological Sorting: Ordering of vertices in a DAG.
  2. Cycle Detection: Using DFS or Union-Find.
  3. Strongly Connected Components (SCC): Identified by using Tarjan’s or Kosaraju’s algorithm
  4. Bipartite Graph Check: Applying coloring techniques and BFS/DFS.

Graph vs Tree in Data Structures

Graphs and trees are not the same, despite their close relationship. Choosing the right structure for a given problem is made easier by being cognizant of its differences.

Similarities

  • Both data structures are non-linear.
  • Both are made up of nodes, or vertices, joined by edges.
  • DFS and other traversal algorithms are valid for both.

Key Differences

Definition

  • Tree: A unique type of connected, acyclic graph.
  • Graph: A broader structure that could have different edge types, cycles, and disconnected parts.

Hierarchy

  • Tree: Displays relationships in a hierarchical manner (e.g., file system, organizational chart)/
  • Graph: Represents broad relationships that are not restricted to hierarchies (e.g., social connections, road networks).

Connectivity

  • Tree: Every node has exactly one path linking it to every other node.
  • Graph: There could be multiple paths, and it could be connected or disconnected.

Cycles

  • Tree: Cannot contain cycles.
  • Graph: It could be acyclic or have cycles.

Number of edges

  • Tree: For every V vertices, there are exactly (V – 1) edges.
  • Graph: An undirected simple graph can contain up to V(V – 1)/2 edges.

When to Use Trees vs Graphs

  • Use a tree when modeling hierarchical data, such as XML documents, file systems, and decision-making processes.
  • Use a graph when modeling arbitrary relationships and connections (such as routes, social interactions, and networks).

Complexity of Graph Operations and Algorithms

The efficiency of operations depends on representation:
  • Adjacency Matrix:
    • Space Complexity: O(V²)
    • Edge Lookup: O(1)
    • Traversal: O(V²)
  • Adjacency List:
    • Space Complexity: O(V+E)
    • Edge Lookup: O(degree of vertex)
    • Traversal: O(V+E)
  • Algorithms:
    • BFS/DFS: O(V+E)
    • Dijkstra (using min-heap): O((V+E) log V)
    • Bellman-Ford: O(VE)
    • Kruskal: O(E log E)
    • Prim: O(E + log V)

Applications of Graphs in Data Structures

Graphs are utilized in multiple real-world applications in many different industries; they are not just theoretical concepts. Graphs are vital in the following important domains:

Social Networks

  • Relationships are edges, and users are vertices.
  • Uses include influencer identification, community detection, and friend recommendations.

Navigation and Route Planning

  • Roads as weighted edges and cities as vertices.
  • Applied to transformation planning and GPS Systems.
  • The fastest and shortest routes are identified by algorithms like Dijkstra and A*.

Web and Search Engines

  • Hyperlinks are edges, and web pages are vertices.
  • To rank pages, graph algorithms such as PageRank assess link structures.

Computer Networks

  • Nodes are devices, and edges are connections.
  • Used in load balancing, network dependability, and routing protocols.

Dependency Management

  • Dependencies as edges and packages, tasks, or modules as vertices.
  • Directed Acyclic Graphs (DAGs) are used in task scheduling and build systems such as Maven and Gradle.

Biology and Chemistry

  • Genes, molecules, or proteins as vertices.
  • Graph theory plays an important role in molecular structure, analysis, and protein-protein interaction networks.

Artificial Intelligence and Machine Learning

  • Graphs are utilized to illustrate states in search problems or relationships in knowledge bases.
  • Used in recommendation systems, semantic search, and graph neural networks (GNNs).

Operating Systems

  • Resources and processes work as vertices.
  • Resource allocation graphs help in the identification and prevention of deadlocks.

The above instances highlight how prevalent graphs are, from biological systems to online platforms, making them an important concept for researchers, engineers, and developers.

Advanced Topics to Read in Graph

Negative Weights and Cycles

  • Bellman-Ford algorithms are used to handle negative edge weights.
  • Negative cycles signify an infinite path cost reduction.

Dynamic Graph

  • Time-varying graphs, such as those detected in dynamic networks or streaming data.

Graph Databases

  • Databases like Neo4j efficiently store and query graph structures.

Graph in Machine Learning

  • Graph Neural Networks (GNNS): Use graph-structured data to extend deep learning.
  • Knowledge Graphs: These are used in AI and semantic search applications.

Interview Questions and Practice Problems

Below are some common graph-related questions asked in interviews:
  • Detect a cycle in a directed or undirected graph.
  • Identify whether a graph is bipartite.
  • Implement DFS and BFS.
  • Find the shortest path in a weighted/unweighted graph.
  • Use the Kruskal/Prim algorithm to construct an MST.
  • Topological sorting of a DAG.
  • In an undirected graph, count the connected elements.

These problems examine both theoretical understanding and real-world application abilities.

Best Practices

In spite of their obvious power, graphs can be hard to use and maintain. Following the best practices below ensures effective, error-free development:

Select the Right Representation

  • To conserve space, utilize an adjacency list for sparse graphs.
  • For dense graphs or situations where fast edge lookups are vital, utilize an adjacency matrix.
  • Take edge lists into account when utilizing algorithms such as Kruskal’s MST.

Improve Storage and Traversal

  • To avoid infinite loops in traversals, always maintain an array or visited set.
  • To maximize memory utility for large graphs, take into account compressed representations (like CSR- Compressed Sparse Row)

Handle Special Cases

  • Exercise caution when utilizing negative edge weights, as not all algorithms (like Dijkstra) support them.
  • Keep an eye out for cycles in directed graphs, especially when topological sorting or dependency resolution is being performed.

Balance Performance and Readability

  • While a recursive DFS is elegant, it can lead to a stack overflow on very large graphs. Consider iterative implementations that utilize explicit stacks.
  • Utilize optimized libraries (like Boost Graph Library in C++ and NetworkX in Python) for applications that need high performance.

Test with Realistic Data

  • To ensure accuracy and scalability, test your graph implementation using both sizable datasets and tiny toys as examples.
  • Continuously look for edge cases, like multiple edges, self-loops, and disconnected graphs.

Think in Terms of Applications

  • Adapt your representation and algorithm selection based on the issue, taking into account factors like maximum flow, connectivity, and shortest path.
  • Before choosing data structures, take into account whether the graph is dynamic (regular updates) or static (unchanging).
  • By adhering to these guidelines, you can ensure that your graph implementations are accurate, scalable, flexible, and efficient enough to manage real-world issues.

Conclusion

Graphs are important in practical problem-solving. They provide strong methods for processing and representing relationships between entities. You can resolve a large number of issues, from network design to AI pathfinding, by understanding different types of graphs detected in data structures, along with their representations, traversals, and algorithms.

Related Reads:

Megana Natarajan