Segment Tree in Data Structures: A Complete Guide
Efficiency is paramount in the world of computer science and competitive programming. Most applications utilize large datasets that necessitate frequent queries and updates. Traditional data structures often fall short in terms of performance when dealing with such applications.
This is where a robust data structure like Segment Tree comes in, providing elegant solutions for range queries and updates in logarithmic time.
| Key Takeaways |
|---|
|
This comprehensive guide on segment trees provides a description of segment trees, including the general concept, how it works, how to build and use it, and explores its variations, applications, and advantages.
What is a Segment Tree?
A segment tree is a binary tree data structure that efficiently handles range queries and point/range updates on an array. It performs operations like finding the sum, minimum, maximum, or other associative operations within a specified range of elements in logarithmic time complexity.

Each node in a segment tree represents an interval or segment of the array. The hierarchical decomposition of a segment tree allows efficient querying and updating of elements because only log(n) segments are processed per operation.
A segment tree is used in cases involving multiple range queries on an array and modifications of elements of the same array. For example, finding the sum of all the elements in a variety from indices 0 to r, or finding the minimum (famously known as the Range Minimum Query problem) of all the elements in a variety from index 0 to N.
Key Components of a Segment Tree
- Binary Tree: The segment tree is organized as a binary tree.
- Root: The root node represents the entire array (
[0, n-1]). - Leaf Nodes: Each leaf node in a segment tree corresponds to a single element of the original input array.
- Internal Nodes: Non-leaf nodes represent segments (ranges) of elements from the array. Each internal node stores aggregated information (e.g., sum, min, max) about the elements within its corresponding segment, derived from its child nodes.
- Array Representation: Segment trees are often implemented using an array, where a node at index
ihas its left child at2*iand its right child at2*i + 1. This means that to accommodate all nodes of a segment tree for an array of sizeN, an array of size approximately4 * Nis required.
Structure of a Segment Tree
A segment tree is a binary tree storing the intervals or segments. Each node in the segment tree is an interval or a range.
- The root of T will be the whole array A[0:N-1].
- Each leaf in T will represent a single element A[i] such that 0<=i<N.
- The internal nodes in the segment tree T represent the union of elementary intervals A[i:j] where 0<=i<j<N.
To start with, the root of the segment tree represents the whole array A[0:N-1]. Then it is divided into two half intervals or segments, and the two children of the root in turn represent the A[0:(N-1)/2] and A[(N-1)/2 + 1:(N-1)].
So, in each step, the segment is divided into two halves, and the two children represent those two halves. So, the height of the segment tree will be log(N). There are N leaves representing the elements of the array. The number of internal nodes is N-1. So, the total number of nodes is 2 x N – 1.
For example, if the size of the tree is 8, the total number of internal nodes = 2x(8-1) = 14.
The general structure of a segment tree for an array of size eight is given below:
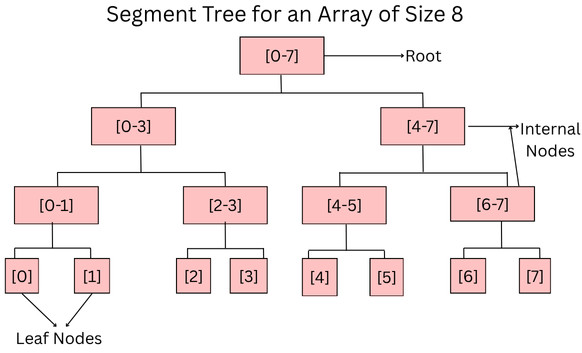
- Update: To update the element of the array (value) and reflect the corresponding change in the segment tree.
- Query: To query on an interval or segment and return the answer to the problem (for example, minimum/maximum/summation in the particular segment).
Example of a Segment Tree
Consider an array A = [2, 4, 1,3, 5]. For this array A, you want to build a segment tree. For this, we proceed as follows:
- Root representing the entire array.
- Leaf nodes represent individual elements of the array.
- Internal nodes represent the sum of the elements in their respective segments, which are the union of the segments of their children.
For the given array A,
- Level 0 (Root): Represents the entire array [0, 4], storing the sum 2+4+1+3+5 = 15.
- Level 1:
- Left child: range [0, 2], sum 2+4+1 = 7.
- Right child: range [3, 4], sum 3+5 = 8.
- Level 2:
- Left child of [0, 2]: Represents [0, 1], sum 2+4 = 6.
- Right child of [0, 2]: Represents [2, 2], sum 1.
- Left child of [3, 4]: Represents [3, 3], sum 3.
- Right child of [3, 4]: Represents [4, 4], sum 5.
- Level 3 (Leaves): Individual elements [0, 0] (2), [1, 1] (4).
Building a Segment Tree
In programming, a segment tree is commonly represented as an array rather than a linked tree for efficiency.
If n is the number of elements in the input array, the segment tree typically requires around 4*n memory space.
Build Process
- If the range
[l, r]is a single element, store that element. - Otherwise, split into two halves:
- Left child →
[l, mid] - Right child →
[mid+1, r]
- Left child →
- Combine the results of the two children (e.g., sum, min, max).
Example Pseudocode for Sum Segment Tree
def build(A, T, node, start, end):
if start == end:
T[node] = A[start]
else:
mid = (start + end) // 2
build(A, T, 2*node, start, mid)
build(A, T, 2*node+1, mid+1, end)
T[node] = T[2*node] + T[2*node+1]
This code recursively builds the segment tree, where T[node] stores the sum of the elements in its range.
The time complexity of this code is O(n), while the space complexity is also O(n).
Segment Tree Operations
- Range Query: Find the sum of elements within a given range [L, R].
- Update: Change the value of an element at a specific index.
Let us discuss both these operations:
Range Query
[L, R] in a segment tree is:- Traverse the segment tree
Tfrom the root. - If a node’s range falls completely within
[L, R], return its stored value. - If a node’s range falls completely outside
[L, R], return a default value (e.g., 0 for sum, infinity for min). - If a node’s range overlaps with
[L, R], recursively query both child nodes and combine their results.
def query(T, node, start, end, L, R):
if R < start or end < L:
return 0
if L <= start and end <= R:
return T[node]
mid = (start + end) // 2
left = query(T, 2*node, start, mid, L, R)
right = query(T, 2*node+1, mid+1, end, L, R)
return left + right
The time complexity for the range query operation is O(log N).
Update (Point or Range)
- Traverse the tree from the root to the relevant leaf node(s). Update the leaf node(s) and then update the values of all ancestor nodes up to the root to reflect the change.
- For range updates, techniques such as Lazy Propagation can be used to efficiently defer updates to child nodes until they are needed, thereby optimizing performance.
def update(A, T, node, start, end, idx, val):
if start == end:
A[idx] = val
T[node] = val
else:
mid = (start + end) // 2
if idx <= mid:
update(A, T, 2*node, start, mid, idx, val)
else:
update(A, T, 2*node+1, mid+1, end, idx, val)
T[node] = T[2*node] + T[2*node+1]
The time complexity for the update operation is O(log N).
Lazy Propagation
In a standard segment tree, updating a range can result in updating all the individual elements within that range. This leads to a time complexity of O(N) per operation in the worst case.
Lazy propagation solves this problem by delaying updates.
Lazy propagation is an optimization technique used in conjunction with segment trees to handle range update operations efficiently.
The primary idea behind this is to defer the updates to child nodes until they are necessary.
- Each node has an associated lazy value.
- When an update over a range [L, R] is made:
- Instead of updating all elements immediately, mark the node as “lazy”.
- Propagate the update when that node is visited later.
- As the query traverses the segment tree, if a node with a pending lazy update is encountered, that update is first pushed down to its children before the query proceeds. This ensures that the query uses up-to-date values.
def update_range(T, lazy, node, start, end, L, R, val):
if lazy[node] != 0:
T[node] += (end - start + 1) * lazy[node]
if start != end:
lazy[2*node] += lazy[node]
lazy[2*node+1] += lazy[node]
lazy[node] = 0
if start > end or start > R or end < L:
return
if L <= start and end <= R:
T[node] += (end - start + 1) * val
if start != end:
lazy[2*node] += val
lazy[2*node+1] += val
return
mid = (start + end) // 2
update_range(T, lazy, 2*node, start, mid, L, R, val)
update_range(T, lazy, 2*node+1, mid+1, end, L, R, val)
T[node] = T[2*node] + T[2*node+1]
With lazy propagation, the time complexity for range updates is O(log n) and for range queries, it is O(log n).
Segment Tree Applications
Segment trees are incredibly versatile. Here are some of their most common applications:
1. Range Queries and Updates
- Range Sum Query: This is the most common use of a segment tree. It efficiently calculates the sum of elements within any range, allowing for updates.
- Range Minimum or Maximum Query: In addition to sums, the minimum or maximum values within a range can also be stored using a segment tree.
For example, a minimum node can be calculated using,
tree[node] = min(tree[2*node], tree[2*node+1]) - Range GCD or LCM Query: Segment trees also handle GCD or LCM operations, enabling efficient number-theoretic queries.
- Range XOR or Bitwise Operations: Segment trees are used in problems involving XOR values across segments.
- Frequency Counting / Mode Queries: Segment trees store frequency maps at each node to answer frequency-related queries.
2. Competitive Programming
A segment tree is a fundamental tool in competitive programming for solving a wider array of problems that involve range-based operations and dynamic array modifications. They are widely used in platforms like Codeforces, LeetCode, and HackerRank for range-based problems.
3. Databases and Search Engines
Segment trees are used to manage indexed data ranges and quickly aggregate results in database and search engine applications.
4. Game Development
Segment trees also help with collision detection, map range updates, and visibility queries, especially in game development.
5. Computational Geometry
- Interval Overlap Detection: Identifying overlaps or intersections between intervals, which are crucial in problems like scheduling or geometric queries.
- 2D Range Queries: Extending segment trees to two dimensions for efficient querying and updates on matrices or grids.
6. Networking and Signal Processing
In the field of networking and signal processing, segment trees are used in segment-based frequency analysis and optimizing dynamic data streams.
7. Other Specialized Applications
- Dynamic Order Statistics: Segment trees are used to support queries for the k-th smallest or largest element in a dynamic array.
- Inversion Count: They calculate the number of inversions in an array, a measure of disorder.
- Persistent Segment Trees: Segment trees maintain historical versions of the data structure, allowing queries on past states of the array.
- Image Processing: Image processing algorithms that require range queries on pixel data or for segmenting images based on various attributes use segment trees.
- Data Analysis: They can be used to analyze large datasets by performing range-based aggregations or statistical computations.
- Financial Applications: Financial functions, such as tracking stock prices, calculating moving averages, or other financial metrics over time, can be performed using segment trees.
Advantages of Segment Trees
- Fast Range Queries: Segment trees allow for efficient retrieval of information about a specific range (e.g., sum, minimum, maximum) in logarithmic time, O(log n).
- Efficient Point Updates: The update operation of a single element in the underlying array is also completed in logarithmic time, O(log n).
- Versatility: Segment trees are versatile and can be adapted to handle various types of range queries and updates, including sum, min, max, GCD, etc..
- Dynamic Data Handling: Updates in segment trees are efficient, and they perform well in scenarios where the underlying data changes frequently.
- Suitable for Large Datasets: The logarithmic time complexity of segment trees makes them highly efficient for processing large datasets.
Disadvantages of Segment Trees
- Complex Implementation: Segment trees are more complicated to implement than simple data structures such as arrays. Recursion and lazy propagation can be error-prone.
- Not Ideal for All Use Cases: Segment trees are not ideal for static data (no updates); simpler approaches, such as prefix sums, may be sufficient.
- Increased Space Complexity: Segment trees require more memory than a simple array, typically around four times the size of the original array, to store the tree nodes, increasing the space complexity.
- Overhead for Small Datasets: When the datasets involved are tiny, the overhead of building and maintaining the tree structure might outweigh the benefits of logarithmic time complexity.
- Slower for Point Updates in Specific Cases: Segment trees are generally efficient; other data structures might offer better performance for certain specific scenarios or widespread point updates.
Variants of Segment Trees
There are numerous variants of segment trees that enhance the basic segment tree's capabilities for more complex range-based problems, such as finding the minimum/maximum in a range or tracking changes over time.
1. Merge Sort Tree
A merge sort tree is a specialized data structure based on a segment tree. It stores a sorted array or vector of all elements present within its corresponding range at each node to handle range-based order statistics queries (like “count of numbers ≤ X”). The merge sort tree is designed to efficiently answer range-based queries needing access to the individual elements in a given range.
2. Persistent Segment Tree
This variant of the segment tree keeps previous versions of the array after updates and is used in problems involving snapshots or history queries. It maintains multiple versions of the data structure. It can also be used to track changes over time by preserving previous states of the tree.
3. 2D Segment Tree
This is an example of a higher dimensions segment tree. 2D segment trees handle data in 2D grids, storing collections of data in two-dimensional spaces, for example, the sum of a submatrix.
4. Dynamic Segment Tree
This type of tree is also known as an implicit segment tree and is used when the array size is not known in advance or is very large. Dynamic segment trees are built dynamically to handle large coordinate spaces or sparse data efficiently. These variants are created on demand as needed, avoiding the need for a pre-allocated, fixed-size array.
Segment Tree Implementation
Segment Tree Implementation in C++
#include <iostream>
#include <vector>
class SegmentTree {
private:
std::vector<int> tree; // Stores the segment tree nodes
std::vector<int> arr; // Original array
int n; // Size of the original array
// Recursive function to build the segment tree
void build(int node, int start, int end) {
if (start == end) { // Leaf node
tree[node] = arr[start];
} else {
int mid = (start + end) / 2;
build(2 * node + 1, start, mid); // Build left child
build(2 * node + 2, mid + 1, end); // Build right child
tree[node] = tree[2 * node + 1] + tree[2 * node + 2]; // Sum of children
}
}
// Recursive function to query the sum in a given range
int query(int node, int start, int end, int l, int r) {
if (r < start || end < l) { // range outside current segment
return 0; // Return neutral element for sum
}
if (l <= start && end <= r) { // completely within query range
return tree[node];
}
int mid = (start + end) / 2;
int p1 = query(2 * node + 1, start, mid, l, r);
int p2 = query(2 * node + 2, mid + 1, end, l, r);
return p1 + p2;
}
// Recursive function to update an element
void update(int node, int start, int end, int idx, int val) {
if (start == end) { // Leaf node, update original array and tree node
arr[idx] = val;
tree[node] = val;
} else {
int mid = (start + end) / 2;
if (start <= idx && idx <= mid) { // Index in left child
update(2 * node + 1, start, mid, idx, val);
} else { // Index in right child
update(2 * node + 2, mid + 1, end, idx, val);
}
tree[node] = tree[2 * node + 1] + tree[2 * node + 2]; //parent sum
}
}
public:
SegmentTree(const std::vector<int>& input_arr) {
arr = input_arr;
n = arr.size();
tree.resize(4 * n); // A segment tree typically needs 4*n space
build(0, 0, n - 1); // Build from root node (index 0)
}
//get sum in a range [l, r]
int getSum(int l, int r) {
if (l < 0 || r >= n || l > r) {
std::cerr << "Invalid query range." << std::endl;
return -1; // Or throw an exception
}
return query(0, 0, n - 1, l, r);
}
// update an element at index idx with new_val
void updateValue(int idx, int new_val) {
if (idx < 0 || idx >= n) {
std::cerr << "Invalid update index." << std::endl;
return;
}
update(0, 0, n - 1, idx, new_val);
}
};
int main() {
std::vector<int> arr = {2, 4, 1, 3, 5};
std::cout << "Original Array: ";
for (int item : arr)
std::cout << item << " ";
std::cout << std::endl;
SegmentTree st(arr);
std::cout << "Sum of elements in range [0, 4]: " << st.getSum(0, 4) << std::endl; // Expected: 3+5+7+9 = 24
st.updateValue(2, 6); // Update element at index 2 (value 5) to 10
std::cout << "Sum of elements in range [0, 4] after updating third value with 6: " << st.getSum(0, 4) << std::endl; // Expected: 3+10+7+9 = 29
return 0;
}
Original Array: 2 4 1 3 5 Sum of elements in range [0, 4]: 15 Sum of elements in range [0, 4] after updating the third value with 6: 20
Segment Tree Implementation in Python
class MinMaxSegmentTree:
def __init__(self, arr):
self.n = len(arr)
# Tree size is typically 4*n for safe indexing
self.tree_min = [0] * (4 * self.n)
self.tree_max = [0] * (4 * self.n)
self.arr = arr
self._build(0, 0, self.n - 1)
def _build(self, node, start, end):
if start == end:
self.tree_min[node] = self.arr[start]
self.tree_max[node] = self.arr[start]
else:
mid = (start + end) // 2
self._build(2 * node + 1, start, mid)
self._build(2 * node + 2, mid + 1, end)
self.tree_min[node] = min(self.tree_min[2 * node + 1], self.tree_min[2 * node + 2])
self.tree_max[node] = max(self.tree_max[2 * node + 1], self.tree_max[2 * node + 2])
def query(self, l, r):
return self._query(0, 0, self.n - 1, l, r)
def _query(self, node, start, end, l, r):
if r < start or end < l: # No overlap
return float('inf'), float('-inf') # Return neutral values
if l <= start and end <= r: # Complete overlap
return self.tree_min[node], self.tree_max[node]
# Partial overlap
mid = (start + end) // 2
min1, max1 = self._query(2 * node + 1, start, mid, l, r)
min2, max2 = self._query(2 * node + 2, mid + 1, end, l, r)
return min(min1, min2), max(max1, max2)
def update(self, idx, val):
self.arr[idx] = val
self._update(0, 0, self.n - 1, idx, val)
def _update(self, node, start, end, idx, val):
if start == end:
self.tree_min[node] = val
self.tree_max[node] = val
else:
mid = (start + end) // 2
if start <= idx <= mid:
self._update(2 * node + 1, start, mid, idx, val)
else:
self._update(2 * node + 2, mid + 1, end, idx, val)
self.tree_min[node] = min(self.tree_min[2 * node + 1], self.tree_min[2 * node + 2])
self.tree_max[node] = max(self.tree_max[2 * node + 1], self.tree_max[2 * node + 2])
if __name__ == "__main__":
arr = [1, 3, 7, 5, 13, 9]
st = MinMaxSegmentTree(arr)
print("Array:", arr)
min_val, max_val = st.query(0, 5)
print(f"Min/Max in range [0, 5]: {min_val}, {max_val}")
min_val, max_val = st.query(1, 3)
print(f"Min/Max in range [1, 3]: {min_val}, {max_val}")
st.update(2, 6)
print("Array after update:", st.arr)
min_val, max_val = st.query(1, 3)
print(f"Min/Max in range [1, 3] after update: {min_val}, {max_val}")
Array: [1, 3, 7, 5, 13, 9] Min/Max in range [0, 5]: 1, 13 Min/Max in range [1, 3]: 3, 7 Array after update: [1, 3, 6, 5, 13, 9] Min/Max in range [1, 3] after update: 3, 6
Conclusion
The segment tree is one of the most versatile, powerful, and efficient data structures in computer science. These trees allow fast range queries and updates by combining recursive decomposition and tree-based storage, and supporting operations far beyond simple sums.
Understanding segment trees equips software professionals with a robust tool for handling a wide range of computational problems efficiently.
|
|
