Arrays in Data Structures: A Complete Guide with Examples & Applications
|
|
Data structures are the backbone of computer science and programming. They provide an organized and efficient way of storing and manipulating program data. Arrays are the most fundamental data structures. Arrays are the building blocks of many advanced data structures and algorithms (DSA) and are essential for anyone learning programming, preparing for technical interviews, or working on DSA.
| Key Takeaways: |
|---|
|
This guide explores the definition, operations, types, applications, advantages, and disadvantages of array data structures.
What are Arrays in Data Structures?
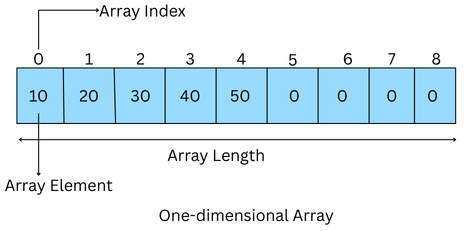
An array is a linear data structure that stores homogeneous elements in contiguous memory locations.
An array contains homogeneous elements arranged in contiguous memory locations. Each element in the array is accessed using an index, with the first element typically stored at index 0. A general structure of an array is shown below:
General Declaration Syntax of Arrays in DSA
data_type array_name[size];
In the above definition:
data_typespecifies the type of data that the array will store. All elements within a single array must be of the same data type, such asintfor integers,floatfor floating-point numbers,charfor characters, or user-defined types likestructs.array_nameis the identifier for the array.sizespecifies the number of elements an array will hold. In languages such as C and C++, the size should be a constant integer known at compile time. The size is determined at run time in other languages, such as Java, that support dynamic arrays.
Memory Representation of Arrays
Arrays occupy contiguous memory blocks, which makes element access very efficient and easy.
Address(arr[i]) = Base_address + (i * size_of_each_element)
1000 and each element is of type int and takes 2 bytes, then arr[3] will be at:1000 + (3 * 2) = 1006
Array Initialization
Specifying values to the array at the time of declaration is known as initializing it. Various programming languages have different ways of initializing arrays.
int arrayOfNum[4]; //Array declaration
int arrayOfNum[4] = {2,4,6,8}; //Array Initialization
import array
# array initialization
myarr = array.array('i', [2,4,6,8])
As the above code snippets show, different programming languages have various ways of declaring and initializing arrays. However, the concept behind the array data structure is the same.
Key Features of an Array
Here are some of the key features of an array:
- Fixed Size: An array is generally of fixed size; once declared, its size cannot be changed in most traditional implementations.
- Contiguous Memory Allocation: Array elements are stored one after another in continuous memory locations, allowing for efficient access.
- Homogeneous Data Type: All elements within a single array must be the same data type (e.g., all integers, all characters, etc.).
- Indexing: Array elements are accessed using an integer index, typically starting from 0 (zero-based indexing). The index is the offset from the array’s base memory address.
-
Random Access: As array elements are stored in contiguous memory locations and accessed using an index, any component of an array can be accessed directly in constant time (O(1)).For example,
if A[4] = {1,2,3,4};is an array.If you want to access its third element, then all you have to do is provide the following statement:int num = A[2];
Types of Arrays in Programming
Arrays come in several forms depending on their structure and dimensions. Main types of arrays are:
1. One-Dimensional Arrays (1D)
A 1D array is the simplest form, often used to represent a list of elements or objects. The elements are arranged in a contiguous block of memory.
marks containing the marks of 5 students. The definition of the marks array is as follows:int marks[5] = {87, 93, 78, 92, 90};
These are the simplest arrays, and elements can be accessed by indexing.
2. Multi-Dimensional Arrays
Data in matrix or tabular form is represented using a multidimensional array containing one or more arrays as its elements.
Most commonly used multidimensional arrays are two-dimensional arrays (2D) or three-dimensional arrays (3D).
-
Two-Dimensional Arrays (2D arrays): These are often used for matrices. A 2D array is defined as follows:
int matrix[2][3] = { {1, 2, 3}, {4, 5, 6} };In the above 2×3 array, the first dimension represents the number of rows, and the second represents the number of columns. The intersection of a row and a column gives the element at that specific location.For example, to access the element with value ‘2’ in the above array, the code is:int num = matrix[0][1];
- Three-Dimensional Arrays (3D): 3D arrays are useful in applications like 3D modeling or storing volumetric data.
One-dimensional and multidimensional arrays are types based on their structure and dimensions. Once defined, the array dimensions remain constant. These are static arrays.
3. Dynamic Arrays
However, some programming languages support dynamic arrays whose dimensions are decided at run time.
Unlike static arrays, dynamic arrays resize automatically as elements are added or removed.
Examples of dynamic arrays are ArrayList in Java and vector in C++.
Array Operations and Algorithms
Several fundamental operations can be performed on arrays. Here are the primary operations:
1. Traversal
Array traversal is visiting every element in an array, one by one, to access, process, or modify its data. Traversal is a fundamental operation for searching, sorting, or printing array elements. It is most commonly achieved using loops such as for, while, or foreach loops to iterate through the array’s indices from the first to the last element.
The time complexity for the traversal operation is O(n).
#include <iostream>
using namespace std;
int main() {
// Write C++ code here
int myArray [5] = {2,4,6,8,10};
cout<<"Array Elements:";
for(int i=0; i<5;i++){
cout << myArray[i] << " ";
}
return 0;
}
Array Elements: 2 4 6 8 10
myArray = [2,4,6,8,10]
print("Linear Array Traversal: ", end=" ")
for i in myArray:
print(i, end=" ")
print()
Linear Array Traversal: 2 4 6 8 10
2. Insertion
Array insertion adds a new element into a pre-existing array, typically requiring shifting existing elements to create space for the new item at the desired position. The process usually involves a loop to shift elements to the right, starting from the end or the insertion point, and then placing the new element into the now-vacant spot.
The operation is pictorially represented as follows:
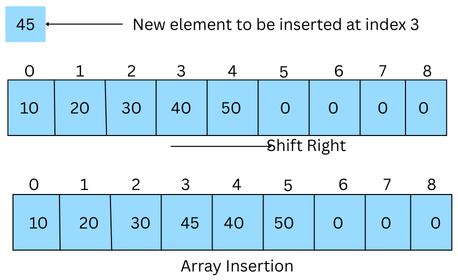
For best case, where an element is inserted at the end (no shifting), the time complexity is O(1) while in worst case (inserting at the start), the time complexity is O(n).
Here, n is the number of elements in the array, because elements must be shifted.
The insertion operation using C++ and Python is shown below:
#include <iostream>
using namespace std;
// Function to insert x in myArray at position pos
int* insertElement(int n, int myArray[], int x, int pos)
{
int i;
n++; // increase the array size by 1 to accommodate new element
// shift elements right
for (i = n; i >= pos; i--)
myArray[i] = myArray[i - 1];
// insert element x at pos
myArray[pos - 1] = x;
return myArray;
}
// Main function
int main()
{
int arr[20] = { 0 };
int i, x, pos, n = 10;
// initial array of size 10
for (i = 0; i < n; i++){
arr[i] = i + 1;
cout << arr[i] << " ";
}
cout << endl;
x = 50; // element to be inserted
pos = 5; // position at which element is to be inserted
insertElement(n, arr, x, pos); // Insert x at pos
// print the array
for (i = 0; i < n + 1; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
1 2 3 4 5 6 7 8 9 10 1 2 3 4 50 5 6 7 8 9 10
myArray = [2,4,6,8,10]
print("Original Array: ", end=" ")
for i in myArray:
print(i, end=" ")
myArray.insert (2,45);
print("\nArray after Insertion: ", end=" ")
for i in myArray:
print(i, end=" ")
Original Array: 2 4 6 8 10 Array after Insertion: 2 4 45 6 8 10
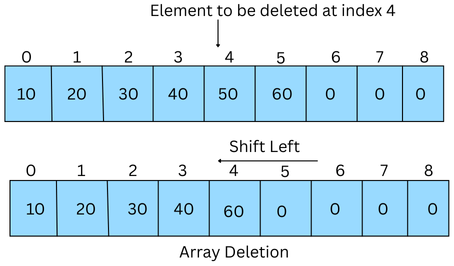
3. Deletion
Array deletion removes an from the array at a specific index. The operation involves shifting the subsequent elements to fill the gap to maintain contiguous data structure.
Deletion of an element from an array is shown in the following figure:
Various programming languages employ different deletion methods. For example, PHP and JavaScript use the splice() function. In C++, an array element is deleted using manual shifting of indices and elements or using the vector<> template of STL.
The best-case complexity for deletion (delete last element) is O(1), while the worst-case complexity (delete first element) is O(n).
The C++ and Python programs for array deletion are as follows:
#include <algorithm>
#include <iostream>
using namespace std;
// Function to delete an element from an array
void deleteElement(int myArray[], int& size, int element)
{
int indexToDelete = -1;
// Find the index of the element to delete, if not found, print message
int* ptr = find(myArray, myArray + size, element);
indexToDelete = ptr - myArray;
if (indexToDelete > size - 1) {
cout << "Element not found in the array." << endl;
return;
}
// Shift elements to the left starting from the index to
// be deleted
for (int i = indexToDelete; i < size - 1; ++i) {
myArray[i] = myArray[i + 1];
}
// Update the size of the array
--size;
}
// main code
int main()
{
int myArray[] = { 20, 50, 10, 90, 30 };
int size = sizeof(myArray) / sizeof(myArray[0]); // Find the array size
cout << "Array before deletion:";
for (int i = 0; i < size; ++i) {
cout << myArray[i] << " ";
}
cout << endl;
int target = 90; // element to be deleted from the array
deleteElement(myArray, size, target); // function to delete the element
// Print the updated array after deletion
cout << "Array after deletion:";
for (int i = 0; i < size; ++i) {
cout << myArray[i] << " ";
}
return 0;
}
Array before deletion:20 50 10 90 30 Array after deletion:20 50 10 30
myArray = [2,4,6,8,10]
print("Original Array: ", end=" ")
for i in myArray:
print(i, end=" ")
myArray.remove (8);
print("\nArray after Deletion: ", end=" ")
for i in myArray:
print(i, end=" ")
Original Array: 2 4 6 8 10 Array after Deletion: 2 4 6 10
4. Searching
The array searching operation finds a specific element in the array. The two methods used for searching an array are linear search and binary search.
-
Linear Search: This is the most common method for searching an element in an array. It iterates through the array from the beginning, comparing each element to the target value till the value is found.The time complexity for linear search is O(n).
-
Binary Search: In this method, it repeatedly divides the search interval in half by calculating the middle element of the array. If the target is less than the middle element, the search continues in the left half; if greater, it continues in the right half. This method is faster than linear search.The time complexity of binary search is O(log n)
#include <iostream>
using namespace std;
int binarySearch(int array[], int x, int low, int high) {
// Repeat until the pointers low and high meet each other
while (low <= high) {
int mid = low + (high - low) / 2;
if (x == array[mid])
return mid;
if (x > array[mid])
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
int main(void) {
int oddArray[] = {1,3,5,7,11,13,15,17};
int x = 5;
int n = sizeof(oddArray) / sizeof(oddArray[0]); //calculate size of array
cout<<"The array to be searched:";
for(int i=0; i<n;i++)
cout<<oddArray[i]<< " ";
int result = binarySearch(oddArray, x, 0, n - 1); //call to binarySearch()
if (result == -1)
cout<< "\nElement not found in array";
else
cout<<"\nElement "<<x<<" is found at index:" << result;
}
The array to be searched: 1 3 5 7 11 13 15 17 Element 5 is found at index:2
def linearSearch(arr, targetVal):
for i in range(len(arr)):
if arr[i] == targetVal:
return i
return -1
myArray = [10, 20,50,30,70,40,90,80,60]
print("Array to be searched: ", end=" ")
for i in myArray:
print(i, end=" ")
print("\n")
x = 40
result = linearSearch(myArray, x)
if result != -1:
print(x, "Found at index", result)
else:
print("Not found")
Array to be searched: 10 20 50 30 70 40 90 80 60 40 Found at index 5
5. Updating an Array
arr[i] = new_value;
Its time complexity is O(1).
Advantages of Arrays
Arrays are fundamental data structures with several advantages:
- Random Access: Since array elements are arranged in contiguous memory locations, elements can be accessed directly using their index, which typically takes constant time (O(1)).
- Memory Efficiency and Cache Performance: Arrays store elements in contiguous memory locations. This spatial locality improves cache performance as frequently accessed elements will likely be in the CPU cache, leading to faster data retrieval.
- Ease of Implementation: Arrays are linear data structures that are simple to understand and implement in most programming languages. Many standard algorithms are naturally designed to work with arrays.
- Foundation for Other Data Structures: Arrays are the building blocks for more complex data structures like stacks, queues, and advanced array-based implementations of trees and graphs.
- Suitability for Algorithms: Many standard algorithms, such as sorting algorithms (e.g., bubble sort, quicksort, merge sort) and searching algorithms (e.g., linear search, binary search), are efficiently implemented using arrays. Binary search, in particular, uses the sorted nature of arrays for logarithmic time complexity.
- Data Organization and Cohesion: Arrays simplify data management and reduce potential errors from scattered data since the data is organized in contiguous memory locations under a single name.
Disadvantages of Arrays
Arrays have several disadvantages as follows:
- Fixed Size: Most arrays have a fixed size that cannot be changed once declared. This inflexibility affects the scenarios where data size changes frequently.
- Expensive Insertion/Deletion: Array operations such as insertion and deletion in the middle of the array are costly and lead to O(n) operations. This is because shifting elements in the middle of the array takes a lot of effort.
- Wasted Memory: Arrays are allocated a size during declaration, so memory is wasted if the array size is larger than needed.
- Homogeneity: Storing only one element type in an array can sometimes be a disadvantage.
Applications of Arrays
Arrays are incredibly versatile and used in multiple domains. Here are the applications of arrays:
- Mathematical Computations: Arrays represent vectors and matrices in mathematical computations. Algebraic expressions, such as polynomial operations and solving linear equations, also use arrays.
- Data Storage: Arrays are used in data storage as they are easily traversed, and accessing random elements is easier. They mainly store records like marks, sensor readings, or temperatures.
- Searching and Sorting: Algorithms like QuickSort, MergeSort, and Binary Search use arrays extensively. Array objects are used extensively in the Standard Template Library (STL) in C++.
- String Manipulation: In languages like C, strings are represented as arrays of characters. The entire string manipulation is performed using arrays.
- CPU Scheduling and Memory Management: Operating systems use arrays in process scheduling and page replacement algorithms.
- Image Processing: In computer vision, images are stored as 2D or 3D arrays (pixels with RGB values), while arrays of vertices can represent 3D models.
- Database Management Systems (DBMS): In DBMS, arrays are used to quickly select, update, and manage multiple records or data points.
Real-World Examples
Arrays are fundamental in computing. They store ordered lists of the same type of data, such as book titles in a library system, paper questions, or intermediate results in an embedded system. Some more real-world examples include:
- Spreadsheets: The rows and columns of a spreadsheet can be viewed as a two-dimensional array of data.
- Compiler Design: Arrays store symbol tables used by the compiler.
- Operating Systems: Arrays manage ready queues and scheduling in operating systems.
- Databases: Indexing in databases often uses array-based structures.
- Networking: Routing tables in networks are implemented with arrays.
- Games: 2D/3D arrays represent game maps or graphics.
Arrays in Different Programming Languages
The following table summarizes arrays in various programming languages:
| Programming Languages | Array Properties |
|---|---|
| C/C++ |
|
| Java |
|
| Python |
|
| JavaScript |
|
Best Practices When Using Arrays
Here are some of the best practices developers should follow when using arrays:
- Choose the Right Size: Avoid allocating vast arrays because you cannot anticipate the exact size beforehand. Choose the right size or the one that more or less matches the actual size.
- Bounds Checking: Avoid accessing invalid array indices in the program.
- Use Dynamic Arrays: When flexibility is needed or when the exact size of the array cannot be determined, use dynamic arrays (if the programming language supports them).
- Prefer Specialized Libraries: For numerical computing, use optimized packages like NumPy.
- Avoid Frequent Shifting Operations: Use linked lists or deques for frequent insertions/deletions, as shifting arrays is too costly.
Conclusion
Arrays are the fundamental data structures in computer science and are the most widely used due to their efficiency in random access and simple implementation. They are indispensable for representing simple lists and complex matrices or forming the basis of advanced data structures and algorithms.
By learning arrays thoroughly, developers can prepare to tackle more advanced structures like stacks, queues, linked lists, and trees, which use arrays in their core implementation. Understanding arrays, their operations, trade-offs, and applications guarantees a solid foundation for academic and real-world programming expertise.
