Searching vs Sorting Algorithms: Key Differences, Types & Applications in DSA
|
|
Searching and sorting are two basic functions that are critical to efficiently solving problems in the domain of data structures and algorithms (DSA). As developers, we often come across scenarios where we must first organize data (sorting) or locate specific data (searching) before conducting additional operations. Both types of algorithms are basic to programming, optimization, and problem-solving, despite their unique functions.
| Key Takeaways: |
|---|
|
Why Focus on Searching & Sorting?
Searching and sorting are always the first options that come to mind when we think of algorithms. Imagine building a library system where you have to decide how to organize the books on the shelves (sorting) and how to find a particular book (searching). When combined, they allow seamless functioning of real-world systems as well as computer programs.
Databases, operating systems, e-commerce websites, and machine learning pipelines are just a few instances of the different applications that implement these algorithms. Because they highlight a candidate’s grasp of efficiency, problem-solving, and analytical thinking, recruiters often test developers on these ideas during interviews. Developers can build code that is scalable, optimized, and easier to maintain by understanding how these algorithms work.
Historical Evolution of Searching and Sorting Algorithms
Knowing the history of these algorithms helps developers understand why computer science places such a significant value on them.
Searching: In early programs and even manual record systems, linear search was the most fundamental type. Binary search modified the game by drastically cutting down on search time with the implementation of ordered data and binary systems.
Sorting: Slower techniques such as bubble sort were leveraged by early mechanical computers. However, the groundwork for efficient data processing was defined by innovations such as Quick Sort (Tony Hoare, 1960) and Merge Sort (John von Neumann, 1945). Due to their capability to adapt to actual data patterns, modern hybrid algorithms such as Timsort are now regularly used in Python and Java.
The Difference Between Sorting and Searching
Let’s start with a simple analogy between searching and sorting before delving deeper:
The main purpose of searching algorithms is to find a particular element in a dataset or to validate whether it exists. For example, locating a student’s record among thousands of records.
Rearranging data elements into a particular order (ascending, descending, lexicographical, etc.) is the objective of sorting algorithms. For example, sorting names in alphabetical order.
- Dependency: Sorting can occasionally be a requirement for searching. Sorting may be a need for rapid searching because binary search, for example, needs sorted input.
- Scalability: Sorting regularly needs an initial investment that is recovered if additional searches are later needed. For instance, sorting once and then using binary search multiple times is more effective than repeatedly searching through unsorted data using linear search.
- Use in Data Structures: Sorting is often needed when comparing datasets, merging information, or aiding binary-like operations, but searching becomes much more efficient when data is structured (trees, hash tables).
Sorting vs. Searching Algorithms
| Aspect | Searching Algorithms | Sorting Algorithms |
|---|---|---|
| Purpose | To find or validate the existence of an element. | To organize all elements in a dataset in a specific order. |
| Input Requirement | Can work on sorted or unsorted data (though efficiency may differ). | Works on all elements, irrespective of order. |
| Output | Boolean (found/not found), position index, or retrieved element. | A dataset arranged in the required order. |
| Time Complexity | O(n) for Linear Search; O(log n) for Binary Search (sorted data). | Ranges from O(n²) (Bubble Sort) to O(n log n) (Merge, Quick Sort). |
| Space Complexity | Minimal (unless advanced structures like trees or hash maps are used). | Varies; some are in-place (e.g., Quick Sort), others need extra memory (e.g., Merge Sort). |
Types of Searching Algorithms
Searching is one of the most popular operations in programming. The selection of algorithms often depends on whether the data is sorted.
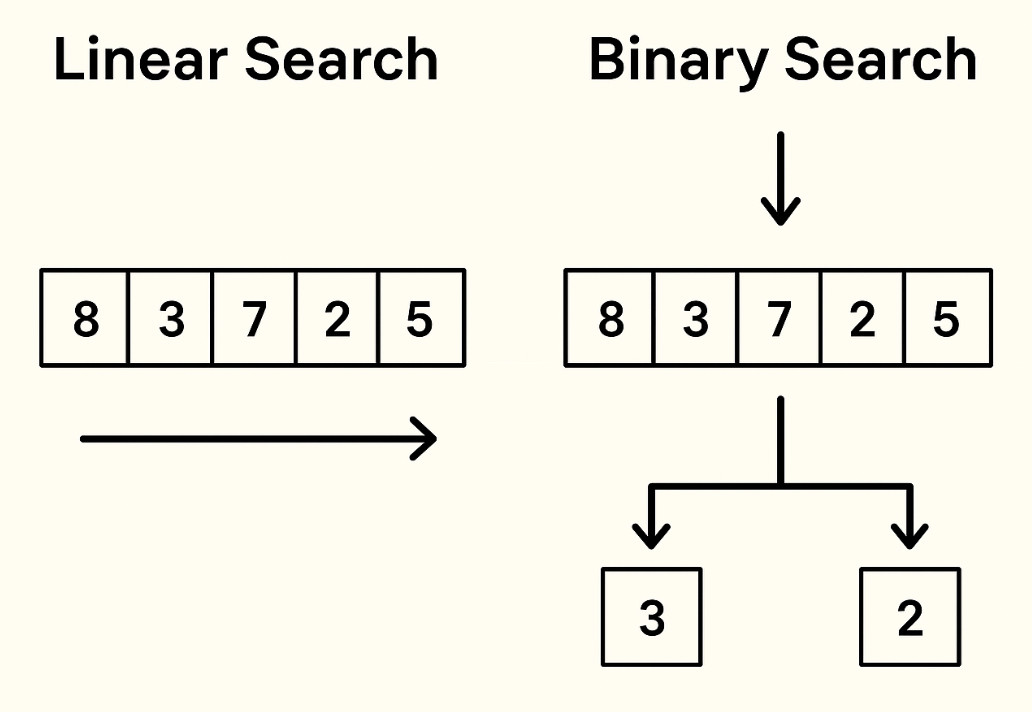
- Linear Search vs. Binary Search
- Linear Search (Sequential Search):
- Scans elements one by one till the target is identified or the end is reached.
- Works on unsorted or sorted data.
- Time Complexity: O(n).
- Example use: Looking up a roll number in a random attendance list.
- Binary Search:
- Needs the dataset to be sorted.
- Continuously divides the search interval into equal halves until the element is identified.
- Time Complexity: O(log n).
- Example use: Searching for a word in a dictionary.
- Linear Search (Sequential Search):
- Hash-Based Searching
- Uses hash functions to achieve near O(1) search complexity.
- Widely utilized in hash tables, symbol tables, and database indexing.
- Tree-Based Searching
- Binary Search Trees (BSTs) and Balanced Trees (AVL, Red-Black Trees) allow effective searching.
- Operations: O(log n) in balanced cases.
- Graph and Specialized Searches
Algorithms like Depth-First Search (DFS) and Breadth-First Search (BFS) are vital for graph-based problems.
Types of Sorting Algorithms
Sorting helps order data to increase efficiency in searching, reporting, and decision-making.
- Bubble Sort vs. Quick Sort
- Bubble Sort:
- Repeatedly swaps adjacent elements till the array is sorted.
- Time Complexity: O(n²).
- Simple to implement but inefficient for large datasets.
- Quick Sort:
- Divide-and-conquer algorithm that chooses a pivot and partitions the array around it.
- Average Time Complexity: O(n log n).
- Preferred in practice due to its speed and in-place sorting.

- Bubble Sort:
- Merge Sort
- Repeatedly divides data and combines them in a sorted order.
- Time Complexity: O(n log n).
- It needs extra space but is stable and efficient.
- Insertion Sort
- Builds the final sorted array one item at a time.
- Time Complexity: O(n²).
- Ideal for small or partially sorted datasets.
- Selection Sort
- Chooses the smallest (or largest) element and organizes it in its correct position.
- Time Complexity: O(n²).
- Heap Sort
- Utilizes a binary heap structure to sort effectively.
- Time Complexity: O(n log n).
- Non-Comparison-based Sorting
- Counting Sort, Radix Sort, Bucket Sort.
- Can achieve O(n) complexity in particular cases.
- Useful for integer or digit-based datasets.
Quick Comparison
- Stable vs. Unstable: While Quick and Heap algorithms may not maintain the relative order of equal elements, Merge and insertion algorithms do.
- Internal vs External Sorting: External sorting manages big datasets that require disk storage, whereas internal algorithms execute in memory (e.g., Merge Sort for external sorting).
- Real-World Use: Libraries often use sorting algorithms, such as Python’s sorted() or Java’s Arrays.sort(), which regularly use hybrid algorithms like Timsort.
Applications of Searching and Sorting in DSA
There are several practical uses for both sorting and searching in computational systems and software development.
Applications of Searching
- Database Operations: These include record retrieval, querying, and validation.
- File Systems: Identifying files using metadata or names.
- Compilers and Interpreters: Hashing is used to look up symbol tables.
- Pathfinding Algorithms: DFS and BFS in navigation systems and game development.
- Search Engines: Index lookups for relevant search terms.
Applications of Sorting
- Data Presentation: Displaying findings in lists that are organized in order (e.g., ranking students by marks).
- Optimization: Efficient searching (Binary Search, range queries) is made possible by pre-sorting.
- Computer Graphics: Rendering algorithms that utilize depth sorting.
- Networking: Establish packet priorities based on their significance.
- Big Data Processing: Sorting is essential in database management systems and MapReduce.
Combined Applications
Both are often used in tandem:
- To apply several binary searches efficiently, a large dataset must first be sorted.
- E-commerce platforms: Searching within filtered results after sorting products per filter (by price, rating).
Importance of Searching and Sorting Algorithms in DSA
Why are these algorithms highlighted by data scientists, engineers, and developers?
- Foundation of DSA: The majority of sophisticated algorithms are basically based on efficient searching and sorting.
- Code Efficiency: When utilized properly, time and space intricacy are decreased, which accelerates up and expands the scalability of applications.
- Problem Solving: Because searching and sorting strategies are vital for solving issues in the real world, they are generally asked about in technical interviews.
- Scalability: Enhanced search and sorting procedures are critical for managing big datasets in modern applications (like databases, search engines, and social media platforms).
- Developer Productivity: It can save time and result in cleaner, more efficient code to understand when to use bubble sort versus quick sort or linear search versus binary search.
Searching vs. Sorting: Which One Matters More?
This relates more to complementary roles rather than a competition between the two:
- Searching-first Viewpoint: Searching is vital if finding or validating data is the immediate goal. For example, establishing whether a username already exists at the time of registration.
- Sorting-first Viewpoint: Sorting results in structured data that aids in faster searching later on when long-term efficiency is required. For example: Facilitating multiple binary searches after sorting employee records once.
The Developer’s Perspective
Both are equally significant for developers. However, context defines when to prioritize one:
- Searching strategies like hashing might be more useful if the data is dynamic (modified often).
- Sorting first ensures faster searches for static data that is accessed regularly.
In addition:
- Interdependency: Sorting regularly serves as a springboard for faster searches. Binary search and other algorithms would not work without sorting.
- Optimization in Practice: Optimal implementations that blend the two are often offered by modern libraries and frameworks. For example, database systems often use sorted arrays with hashing or binary search trees.
- Interview Relevance: Candidates may be required to display their knowledge of sort and then search during tech interviews, which helps demonstrate their grasp of trade-offs.
Complexity Analysis of Searching and Sorting Algorithms
Both time complexity and space complexity are significant factors to take into account when assessing algorithms.
Time Complexity Overview
- Searching:
- Linear Search: O(n)
- Binary Search: O(log n)
- Hash-based Search: Average O(1), Worst-case O(n)
- Tree-based Search: O(log n) for balanced trees
- Sorting:
- Bubble, Selection, Insertion Sort: O(n²)
- Merge, Quick, Heap Sort: O(n log n)
- Counting, Radix Sort: O(n) under specific conditions
Space Complexity Overview
- In-place algorithms (e.g., Quick Sort, Heap Sort) use consistent extra space.
- Non-in-place algorithms (e.g., Merge Sort, Counting Sort) need additional memory.
Trade-offs: Developers often have to choose between algorithms that are slower but more memory-efficient and those that are faster but need more memory. For example, Quick Sort is usually faster but unstable, whereas Merge Sort is stable and predictable, but eats up more memory.
Real-World Case Studies
- E-commerce Platforms: When you search for a product on Amazon, here are the steps.
- First, products are sorted by filters like rating or price.
- Then, specific items that match keywords are retrieved by searching algorithms.
- Search Engines: Google has billions of pages in its index.
- Sorting enables results to be ranked according to their relevance.
- Searching efficiently identifies documents that match user queries.
- Operating Systems
- Sorting is utilized in CPU scheduling to understand which process is offered priority.
- To find and open files fast, file systems depend on searching.
- Social Media Platforms
- Searching helps users find friends, hashtags, or posts faster.
- Sorting helps in organizing feeds by time or relevance.
Best Practices for Developers
- Choose Based on Data Size
- For small datasets, linear search or insertion sort might be sufficient.
- For large datasets, Binary Search, Merge Sort, or Quick Sort perform better.
- Consider Data Nature
- Binary search was leveraged to sort the data.
- Data that is almost sorted: Insertion Sort works efficiently.
- Random data: Quick Sort or Heap Sort.
- Strike a Balance between Memory and Speed
- When memory is at a premium, use in-place algorithms.
- When data stability is important, select stable algorithms (e.g., sorting records by multiple fields).
- Make Use of Built-in Libraries: The majority of modern languages offer enhanced implementations (such as Python’s sorted() with Timsort()).
Future of Sorting and Searching
Searching and sorting are evolving as big data and AI systems become more prevalent:
- Distributed and Parallel Sorting: Sorting across clusters is made possible by algorithms developed for distributed systems, such as Spark and Hadoop.
- Machine Learning Assisted Searching: AI-powered systems predict probable matches in place of traditional searching, which reduces the need for brute-force checks.
- Quantum Algorithms: With near-immediate searching and sorting for bigger datasets, quantum computing may reshape complexity in the future.
Conclusion
Both sorting and searching algorithms are necessary in DSA. Developers can build more efficient and scalable systems by knowing the types of sorting and searching, as well as their applications. Every developer who wants to build high-quality code must understand these basics, whether it’s deciding between binary and linear search for a dataset or bubble sort and quick sort for element ordering.
Developers who understand the real value of searching and sorting algorithms work better in real-world applications that need accuracy, scalability, and performance, as well as in coding interviews.
