Tree in Data Structures: A Complete Guide with Types, Traversals & Applications
In computer science, trees are one of the most fundamental and versatile data structures. Trees fuel many vital algorithms and applications, from storing hierarchical data such as file systems and organizational charts. Additionally, it aids efficient searching and sorting through structures such as binary search trees and B-trees. The basic idea, types, operations, and practical applications of trees in data structures will all be covered in this blog.
| Key Takeaways: |
|---|
|
Introduction to Tree Data Structures
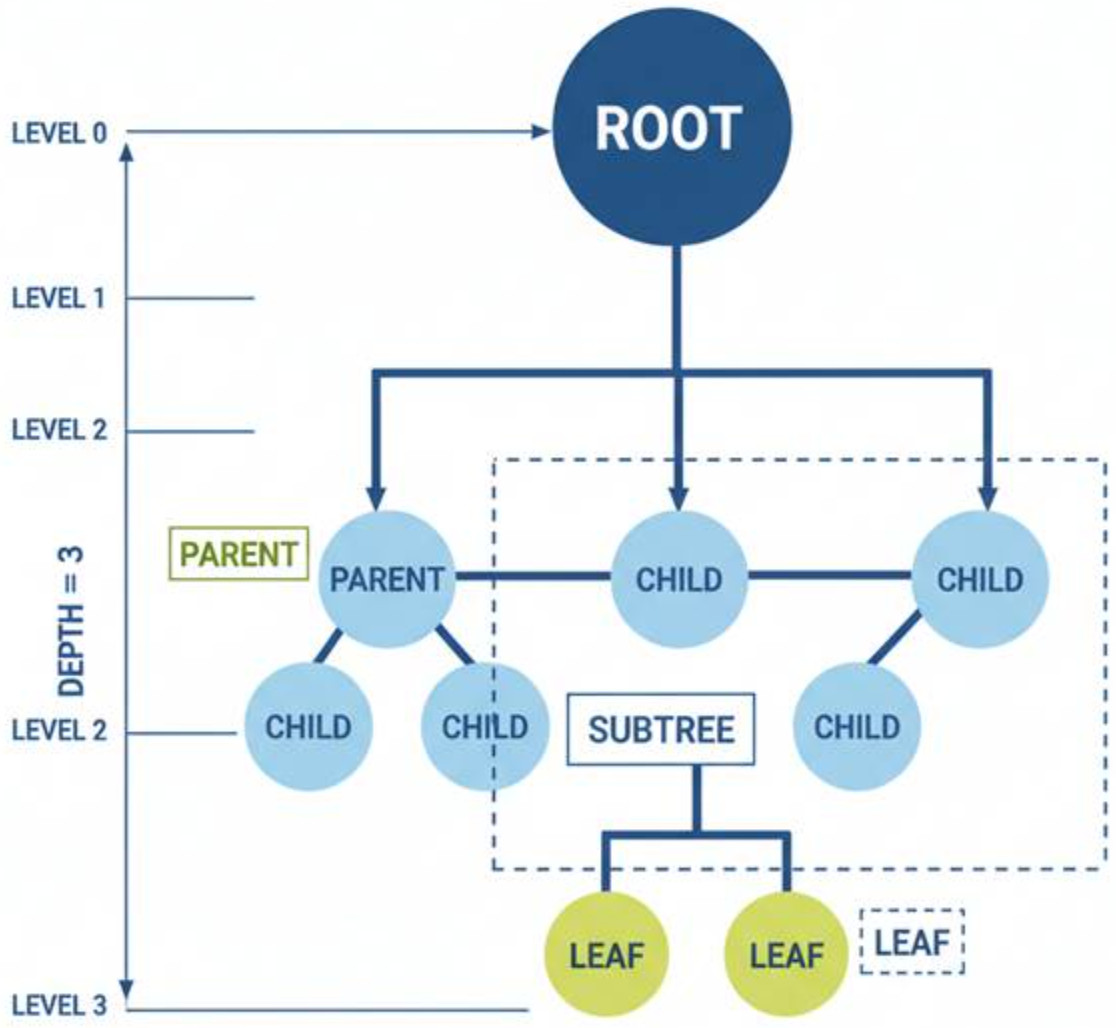
A non-linear data structure that highlights hierarchical relationships is called a tree. A tree consists of nodes connected by edges that form a hierarchy, as compared to the linear nature of arrays, linked lists, or stacks.
- Node: A tree’s basic unit.
- Root: The highest node.
- Edge: The joining of two nodes.
- Parent and Child: A node that is connected below and above.
- Leaf: A node without children.
- Height: The longest path between a root and a leaf.
- Level/Depth: Distance from a root.
- Subtree: A tree formed by a node and its descendants.
These terms serve as the basic foundation for understanding different tree types and functions.
Why Use a Tree Data Structure?
- File systems (folders inside folders).
- HTML/ XML DOM representation.
- Database indexing (B-trees, B+ trees).
- Network routing.
- Compilers (expression trees).
When correctly balanced, trees enable logarithmic search and insertion times when compared to linear structures.
Properties of Trees
- A tree with n nodes has exactly n-1 edges.
- The root has no parent.
- Every node (except the root) has exactly one parent.
- Trees can be recursive, i.e., each child node can itself be the root of a subtree.
Types of Trees in Data Structures
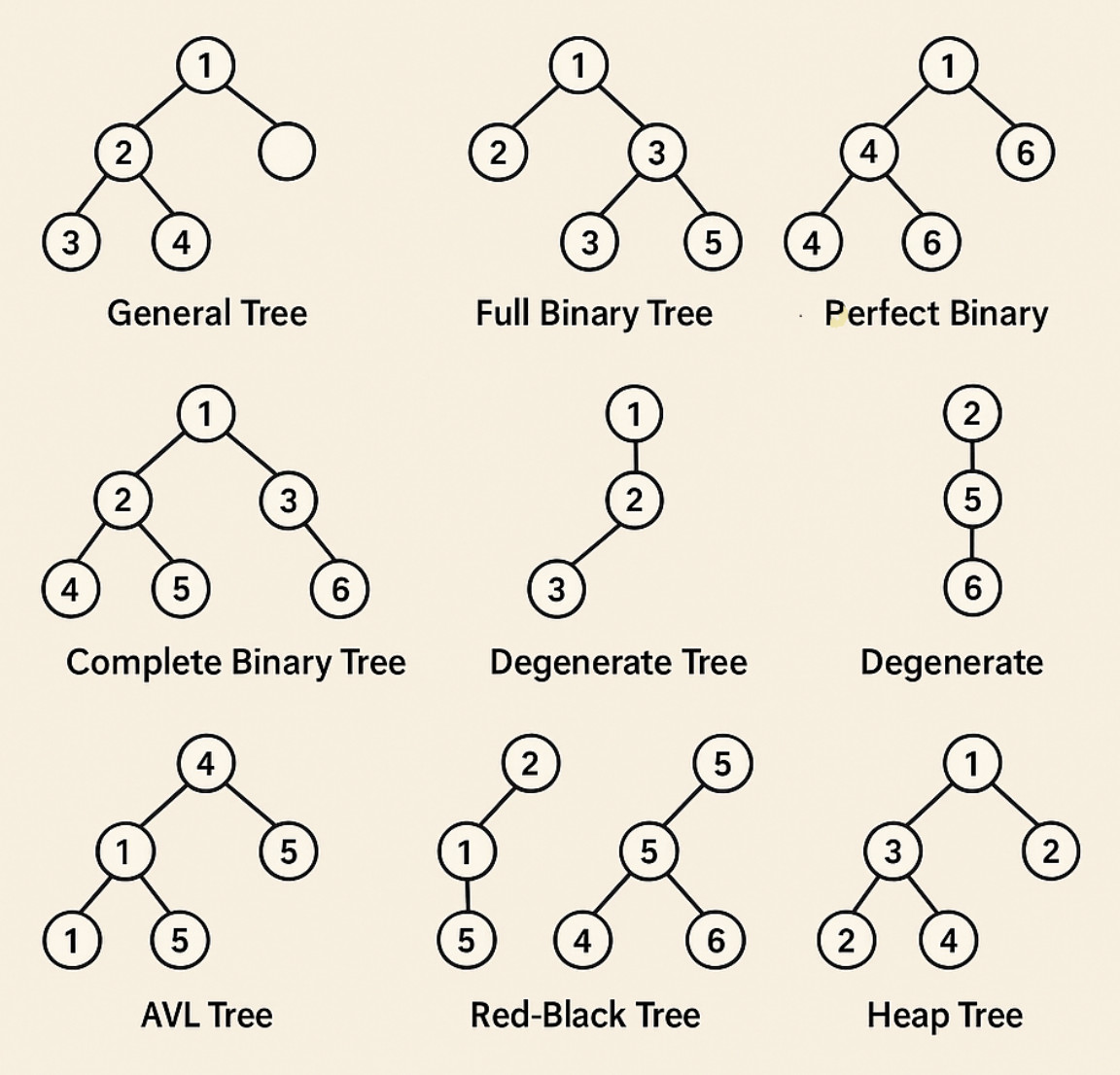
There are multiple varieties of trees, each one customized to solve a unique set of problems. The most important ones, along with their characteristics, functions, and practical applications, will be explored below.
General Tree / N-ary Tree
Definition: A general tree, also called an N-ary tree, is one in which each node may have an arbitrary number of children. An n-ary tree is one in which each node can have no more than n children.
Representation: To store an arbitrary number of children in a binary form, the left-child right-sibling representation is often used.
- Representing hierarchies within organizations.
- DOM structures in XML and HTML.
- Game trees in AI (similar to chess).
Binary Tree
Definition: Usually called left and right, each node can have a maximum of two children.
- Full Binary Types: Each node has either 0 or 2 children.
- Perfect Binary Tree: Each leaf is at the same depth, and every internal node has two children.
- Complete Binary Tree: Every level is completed, with the potential exception of the final one, which is filled from left to right.
- Degenerate/ Skewed Tree: All nodes form a single chain, either left-skewed or right-skewed.
- Expression trees in compilers.
- Intermediate structures for heaps and balanced search trees.
Binary Search Tree (BST)
Definition: A binary in which the right child is larger than the parent and the left child is smaller. This property applies recursively to all subtrees.
- Search, insertion, and deletion can be done in \(O(h)\), where \(h\) is the height.
Edge Case: If unbalanced, BST may deteriorate to a linked list with \(O(n)\) performance.
- Dictionaries and ordered maps.
- Autocomplete engines (with changes like balanced BSTs).
Balanced Trees
Balanced trees ensure logarithmic time complexity by maintaining constraints on height.
- AVL Tree:
- Each node keeps a balance factor (the difference in height between left and right subtrees).
- Imbalances are resolved with rotations (LL, RR, LR, RL).
- Use Case: Situations with heavy search operations needing fast lookups.
- Red-Black Tree:
- Nodes are colored red or black, adhering to rules (no two consecutive reds, same black height on all paths).
- Slightly more flexible than AVL, fewer rotations required.
- Use Case: Widely used in libraries (Java’s TreeMap, C++ map, Linux kernel).
Comparison: AVL encourages searches (stricter balance), while Red-Black encourages insertions and deletions (reduced rebalances).
Heap Trees
- Min-Heap: Parent ≤ children.
- Max-Heap: Parent ≥ children.
- Used for priority queuing (heapq in Python, PriorityQueue in Java).
- Heap sort algorithm.
- Scheduling in operating systems.
B-Trees and B+ Trees
- B-Tree: A self-balancing search tree enabling multiple children per node. Utilized when data does not fit in memory and needs disk storage optimization.
- B+ Tree: An extension where all values are stored at the leaf level, and internal nodes only contain keys for guiding searches. For quick range queries, leaves are linked.
- Databases (MySQL, PostgreSQL).
- File systems (NTFS, ext4).
Tries (Prefix Trees)
Definition: A multi-way tree storing strings where each edge defines a character.
Operations: Insert and search operations take \(O(m)\), where \(m\) defines the length of the word.
- Autocomplete engines.
- Spell checkers.
- IP routing (longest prefix match).
Specialized Trees
- Segment Tree: Allows for range queries (sum, min, max) and updates in \(O(\log n)\).
- Fenwick Tree (Binary Indexed Tree): Similar to a segment tree but simpler, for prefix sums.
- Suffix Tree: Utilized for fast substring searches and pattern matching.
- Decision Trees: Well-known in machine learning for classification and regression tasks.
Representation of Trees
Pointer Representation
Each node contains data and references to its children.
Array Representation
- Root at index 0.
- For node at index i:
- Left child → 2i+1
- Right child → 2i+2
Left-Child Right-Sibling Representation
Ideal for illustrating in general n-ary trees.
Tree Traversal Algorithms in Data Structures
- Depth-First Traversal
- Preorder: Root → Left → Right
- Inorder: Left → Root → Right
- Postorder: Left → Right → Root
- Breadth-First Traversal
- Level Order Traversal: Use a queue to visit nodes one level at a time.
For many tree algorithms and interview questions, traversal techniques are vital.
Operations on Binary Search Tree (BST)
Maintaining BST order, install the new node.
Move on to the left or right after comparing the key with the root.
- Node with no children → eliminate directly.
- Node with one child → replace with child.
- Node with two children → replace with the correct inorder successor.
Maximum: Move right until null.
Operations on Balanced Trees
Rotations during insertion and deletion are handled by balanced trees such as Red-Black Trees and AVL.
AVL Rotations: Single and double rotations resolve imbalances.
Red-Black Trees: Use coloring rules (no two consecutive red nodes, black-height property).
These ensure O(log n) performance.
Complexity Analysis
| Operation | BST (Unbalanced) | Balanced Trees |
|---|---|---|
| Search | O(h), worst O(n) | O(log n) |
| Insert | O(h), worst O(n) | O(log n) |
| Delete | O(h), worst O(n) | O(log n) |
Here h is the height of the tree.
Applications of Trees in Data Structures
- File Systems
- Files and folders are organized hierarchically.
- Databases
- B-trees for indexing.
- Use B+ Trees for range queries.
- Compilers
- Arithmetic expression assessment using expression trees.
- Networks Routing
- Spanning trees and routing tables.
- Artificial Intelligence
- Decision trees for classification hurdles.
- String Processing
- Tries and suffix trees are utilized for autocomplete, search, and pattern matching.
Advanced Trees
- These are used for range queries like max, min, and sum.
- Supports updates in O(log n)
- Efficient cumulative frequency sums.
- Pattern matching in linear time.
Competitive programming makes extensive use of these innovative structures.
Edge Cases and Trade-offs
- Degenerate Trees: Sorting the data converts the BST into a linked list.
- Balancing Cost: Overhead is boosted by balancing operations.
- Memory Overhead: Additional metadata is stored by balanced trees.
The use cases decide which tree is best.
Tree Problems in Interviews
- Serialize and deserialize a binary tree.
- Calculate the diameter of a tree.
- Lowest common ancestor (LCA).
- Maximum path sum.
- Mirror or invert a binary tree.
Both theory and coding capabilities are examined by these problems.
Use Cases and Practical Applications
-
Operating systems and file systemsHierarchical File Structure: Trees are used to represent directories and subdirectories. Files and leaves are terminal nodes, and each folder is a node.
Root ├── Documents │ ├── Resume.pdf │ └── Report.docx └── Pictures ├── Vacation │ ├── photo1.jpg │ └── photo2.jpg └── Family └── photo3.jpg - Permission Management: Permission inheritance between directories works quite similarly to a tree traversal in Unix-like systems.
-
DatabasesB- Tree and B+ Trees: Popularly used for indexing big data sets. They effectively allow logarithmic access to rows and range queries.B+ Tree Diagram (Order 3):
[10 | 20] / | \ [5,8] [12,15,18] [22,25,30]Transaction Management: Dependencies between operations can be tracked by trees. -
Networking
- Routing Algorithms: Efficient network paths are established by spanning trees.
- DNS Hierarchy: In truth, the Domain Name System is a tree structure.
-
Artificial Intelligence and Machine Learning
- Decision trees: Regularly used for tasks involving regression and classification.
Example:[10 | 20] / | \ [5,8] [12,15,18] [22,25,30] -
Web Development
- DOM (Document Object Model): A tree that represents the HTML structure of web pages.
-
Compilers and Expression Evaluation
- Abstract Syntax Trees (AST): These represent mathematical expressions.
* / \ + 2 / \ 3 5
-
Search Engines & Information Retrieval
- Tries: Utilized for effective dictionary and autocomplete suggestions.
Example:(root) └── c └── a ├── t (word: "cat") └── r └── t (word: "cart")
Common Pitfalls, Interview Myths, and Edge Cases
Even though trees are well-defined, learners and practitioners frequently face confusion. Let’s address the most typical pitfalls.
- Height: Distance from a node to the deepest leaf.
- Depth: Distance from the root to the node.
A (depth=0, height=2) / \ B C (depth=1) / D (depth=2, height=0)
Full Binary Tree:
A
/ \
B C
Complete Binary Tree:
A
/ \
B C
/
D
Perfect Binary Tree:
A
/ \
B C
Memory Overhead Misconceptions
Trees are heavier than array-based representations because each node entails multiple references. Arrays may be more efficient for dense datasets:
Interview Myths
- “AVL Trees are always better than Red-Black Trees.” à AVL has more rotations but more strict balancing.
- “Tries are always perfect for strings.” à They use a lot of memory with sparse alphabets.
Edge Cases
- Empty trees need to be managed carefully.
- Clear policies are required for duplicate keys (store counts or always insert right).
- In large trees, recursion depth may lead to stack overflow; iterative traversals are safer.
Additional Topics for Optional/ Additional Reading
Here are some advanced tree structures and concepts for users who wish to explore further.
- Maintain versions of trees after updates.
- Use case: Range sums with historical queries.
- Randomized BST using priorities.
- Regularly accessed elements shift closer to the root.
- Benefit: Ideal for caching systems.
- Utilized for overlapping intervals.
- Example: Intervals [(5,10), (15,20), (25,30)] stored in a tree to respond to overlap queries faster.
- A combination of heap and inorder traversal.
- Use case: Range Minimum Queries (RMQ).
- A balanced height should be the basis for B-trees.
- Supports dynamic graph queries.
Reduces costly I/O operations by optimizing for disk-based storage.
Conclusion
The base of many algorithms and real-world systems consists of trees in data structures. A solid understanding of trees is critical whether you are working with databases, enhancing search algorithms, or getting ready for coding interviews. Trees are the base of many real-world systems, so they are not just a theoretical idea. Beyond their basic structures, knowing advanced trees, conventional pitfalls, and a range of applications gives the skills needed to successfully handle theoretical and real-world issues.
|
|
