Window Sliding Technique in Data Structures Explained

In data structures, the window sliding technique is an enhancement method used to reduce the time complexity of subarray or substring problems. This method allows you to “slide” a window across the data, reusing the outcomes of previous calculations, as compared to repeatedly recalculating values for each window or segment.

The sliding window algorithm essentially keeps a window, a subset of adjacent elements, moving across the input. We avoid duplication of effort by incrementally updating the state (like counts, sums, or character frequencies) as elements come in or go out of the window. Because of this, the method is highly useful for problems needing high efficiency, like those where the input size is around 10⁵ or 10⁶.

You see a continuous, shifting view, but only a segment of the scenery at a time, much like when you look out of a moving train window. This shifting window allows us to monitor only the relevant data segment in computer science without having to go over the complete set again.

Key Takeaways:
  • The sliding window technique is a powerful method for processing contiguous segments (subarrays or substrings) efficiently by reusing computations.
  • There are two main variants: fixed-size window (window size predetermined) and variable-size window (dynamic expansion/contraction based on constraints).
  • In fixed-size problems, you compute the first window and then slide it by subtracting the outgoing and adding the incoming element.
  • In variable-size problems, you maintain two pointers (left, right) and adjust them to satisfy constraints (e.g., sum ≥ target, uniqueness).
  • Look for a sliding window when problems involve contiguous segments, maximizing or minimizing something, and can support incremental updates.
  • The sliding window algorithm cuts down time complexity from potential O(n²) or O(n·k) to O(n).
  • It’s memory efficient (uses O(1) or minimal extra space), and works across arrays, strings, streaming data, and even network protocols.
  • Be cautious of pitfalls: pointer mismanagement, negative numbers (breaking monotonicity), non-contiguous dependencies, or operations that aren’t constant time.
  • In computer networks, a sliding window underpins protocols like TCP for flow control and reliability — the same “window slides forward as data arrives.”
  • Mastering sliding windows will help in interviews, real-world algorithms, streaming analytics, and system design.

Introduction to the Sliding Window in Data Structures

One vital method often used in algorithm design is the sliding window in data structures. It is based on two fundamental ideas:
  • Reusability of Previous Computation: We change the previous result by subtracting the element leaving the window and adding the element entering it, rather than recalculating values for each new subarray or substring.
  • Contiguity of Data: Typically, the issues concern contiguous data blocks, such as substrings in strings or subarrays in arrays.

Take, for example, calculating the average of each size k subarray. The sliding window technique eliminates redundancy by utilizing the sum of the previous window to compute the subsequent one in constant time, as compared to a naïve method that would repeatedly calculate sums for overlapping subarrays.

Because of this, the sliding window algorithm is often used to solve range queries, pattern searches, and other issues involving dataset processing.

Why the Sliding Window Technique Matters

The sliding window method is critical for a number of reasons:

Time Complexity Improvement

It is often possible to decrease problems that would otherwise take O(n x k) or O(n²) time to O(n). In large-scale applications like the analysis of logs, DNA sequences, or real-time data streams, this is vital.

Memory Efficiency

The method is lightweight in comparison to solutions that call for extra arrays or matrices because it only utilizes a small number of variables (running sums, counters, or hash maps).

Versatility

Issues with sliding windows occur in many domains:
  • Arrays (finding averages, max/min sum subarrays).
  • Real-time systems (moving averages).
  • Strings (longest substring without repeating characters).
  • Networking (packet transmission and flow control).

Practical Relevance

The method is not just theoretical. Recommendation systems, anomaly detection in streams, and packet handling in computer networks are just a few instances of its multiple industrial applications.

To put it briefly, the sliding window technique converts clumsy, unscalable solutions into innovative, effective algorithms.

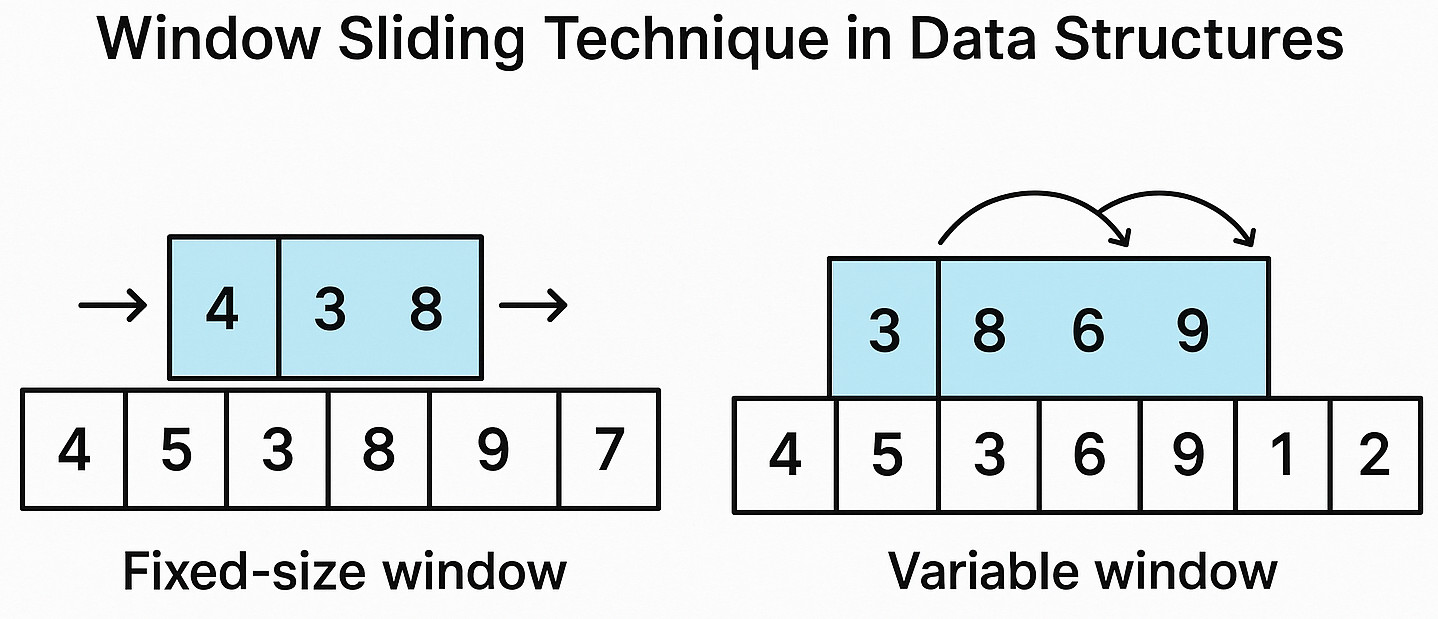
Types of Sliding Window Technique

Typically, sliding window problems can be segregated into two major groups:

  1. Fixed-size Sliding Window

    • Definition: The window size is predetermined and stays the same during the algorithm.
    • Examples: It includes rolling averages, k-radius averages, and the maximum sum of subarrays of size k.
    • Benefits: Very efficient and easy to implement.
    • Implementation: As the window slides, add one new element and remove one old element to update the sum (or other relevant metric) of the first window.

  2. Variable-size Sliding Window

    • Definition: Depending on the circumstances of the issue, the window size is dynamic.
    • Examples: It includes the smallest subarray with sum ≥ target and the longest substring without character repetition.
    • Benefits: More flexible and powerful, able to address an increased variety of issues.
    • Implementation: To scale or contract the window until the constraints are met, use the left and right pointers.

Selecting Between Variable and Fixed

  • Use fixed-size if the problem specifically calls for a window length.
  • A variable window is often needed if the problem refers to “at most”, “minimum length,” or “longest substring.”

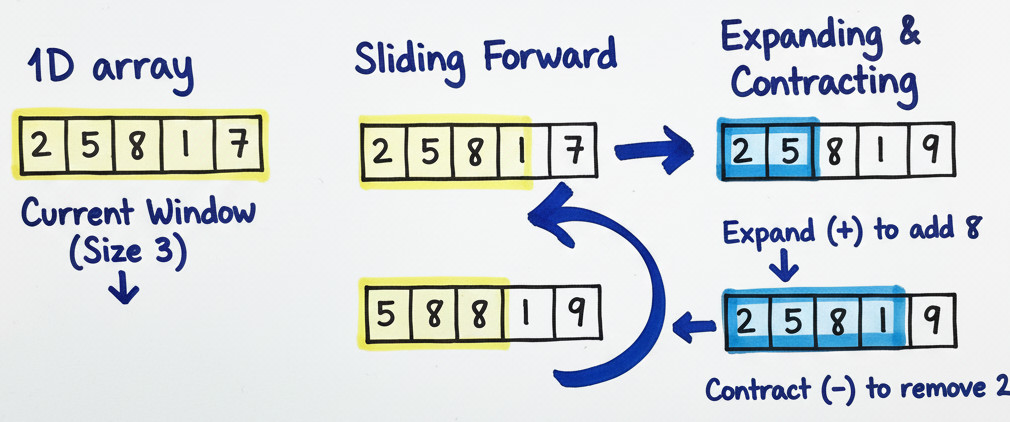
Working of the Sliding Window Algorithm

Let’s explore the sliding window algorithm in detail:
  • Initialization: Begin by initializing the array with pointers.
  • Expansion: To add new elements to the window, move the right pointer.
  • Update State: Keep track of variables like frequency counts, running sums, and maximum/minimum values.
  • Contraction: Move the left pointer to make the window smaller when a condition is met or optimization is feasible.
  • Document Outcomes: Update the final response (e.g., maximum sum, shortest length, longest substring) at each valid step.

This pattern leads to linear complexity by enabling each element to be processed no more than twice: Once when entering the window and once when exiting.

Examples of Sliding Window Problems

  • Maximum Sum Subarray of Size K: Identifying the maximum sum across all subarrays of size k is a classic fixed-size problem. Efficiently resolved with a sliding window in O(n).
  • Longest Substring Without Repeating Characters: A variable-size problem. When a character repeats, the window shrinks to the left and expands to the right.
  • Smallest Subarray with Sum ≥ Target: To find the minimum length subarray, we first expand the window until it reaches or exceeds the goal, and then we shrink it.
  • Anagram Detection: We can check if a string contains an anagram of another by using a sliding window with character frequency counts.
  • Maximum of All Subarrays of Size K: A slightly more sophisticated form of a fixed-size sliding window, where the maximum number of elements can be tracked using a deque (double-ended queue).

These issues display how the same method can be applied to both simple and complex algorithmic problems.

Sliding Window in Computer Networks

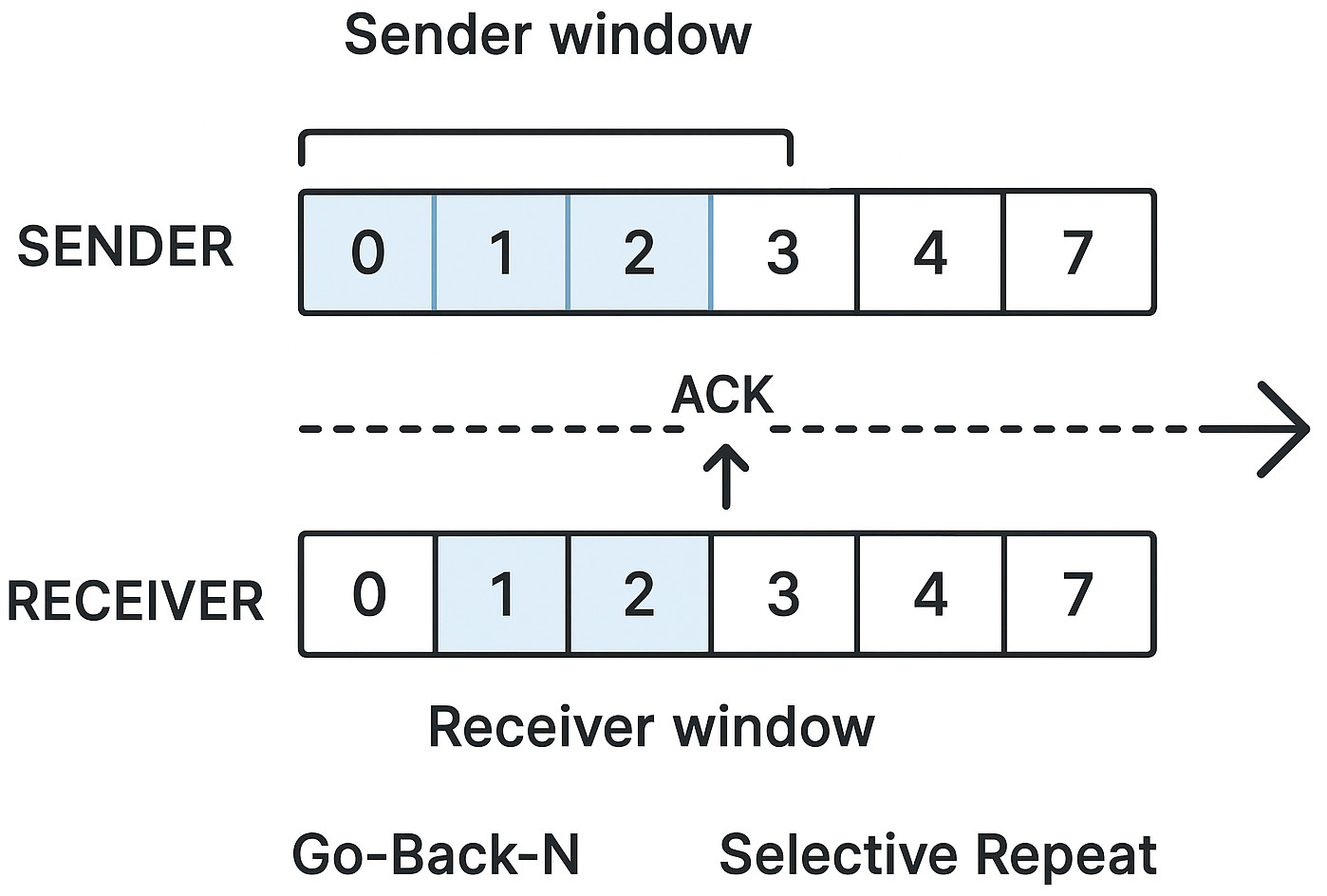
The sliding window technique is necessary for dependable and effective communication in computer networks, especially in the Transmission Control Protocol (TCP).

How it works:
  • A sender keeps track of a window of frames or packets that can be sent without waiting for confirmation.
  • The sender slides the window forward in response to the receiver acknowledging received packets.
  • The sender only retransmits the unacknowledged packets in the event that packets are lost.
Benefits of Networking:
  • Effectiveness: Stops the sender from waiting pointlessly for each packet to be acknowledged.
  • Flow Control: Modifies the window’s size as per the receiver’s capacity.
  • Error Handling: Enhances performance by retransmitting only lost packets.

This highlights the conceptual alignment between sliding windows in data structures and computer networks, as both seek to maximize performance by maintaining a controllable, rolling context.

Recognizing Sliding Window Problems

Knowing when this technique works is one of the most difficult aspects of using it. Here are some clues:
  • Contiguous subarrays or substrings are at the heart of the issue.
  • Over a contiguous segment, the problem requests the longest, shortest, maximum, and minimum.
  • Limits or thresholds are used in constraints (e.g., sum ≥ target, at most k distinct characters).
  • Given the size of the input, O(n2) is probably not feasible.
  • Updates can be made incrementally, by adding one new element and eliminating one old one.

Developers can save time by learning to recognize these patterns and using the sliding window technique right away.

Benefits of the Sliding Window Approach

  • Speed: It converts inefficient O(n) algorithms from brute-force O(n²) solutions.
  • Memory Efficiency: It uses minimal auxiliary structures (such as hash maps) for variable-size problems and constant extra space for fixed-size problems.
  • Flexibility: Adapts to frequency analysis, substring uniqueness, maximum/minimum values, sums, averages, and more.
  • Relevance Across Domains: Used in time-series analysis, algorithms, TCP/IP networking, and machine learning preprocessing (such as rolling averages).
  • Scalability: It is ready for production because it can handle inputs that are 10⁵ in size or larger.

Pitfalls to Watch Out For

Although efficient, the sliding window method can be tricky:
  • Wrong Window Size (Fixed-size): Inaccurate results may arise if you slide the window without properly updating it.
  • Pointer Mismanagement (Variable-size): Inadequate management of the left and right pointers may lead to infinite loops or skipped segments.
  • Negative Numbers: While some sliding window problems need non-negative values, monotonic assumptions may be broken by negative numbers.
  • Overcomplication: While some issues may seem to be sliding window issues, they actually demand alternative strategies, such as dynamic programming.
  • Edge Cases: Careful handling is needed for empty arrays, extremely small input sizes, and values of k greater than n.

Developers can rightly implement the sliding window method and steer clear of common mistakes by being aware of these pitfalls.

Sliding Window vs. Other Techniques

Despite the sliding window algorithm’s strength, it is critical to differentiate it from other widely used methods:

Sliding Window vs. Divide and Conquer

  • Contiguous, incremental issues can be solved with a sliding window.
  • For recursive subproblem breakdowns, such as merge sort, divide and conquer works better.

Sliding Window vs. Dynamic Programming

  • The sliding windows only function when updates are constant-time, but they avoid recomputation.
  • Although dynamic programming provides greater flexibility, it might necessitate O(n²) states or transitions.

Sliding Window vs. Prefix Sum

  • For range queries, prefix sums calculate cumulative totals in advance.
  • Sliding windows work better with variable-size windows and use less memory.

When Sliding Window Doesn’t Work

The sliding window method is flexible, but it has drawbacks:
  • Non-contiguous Problems: Sliding windows cannot be used to solve problems that call for non-contiguous selections, such as subsets.
  • Complex Dependencies: The sliding window technique may not work if a window’s value is influenced by global factors in addition to local ones.
  • Heavy Operations per Update: The efficiency gains are decreased if the window rate is updated in a non-constant-time manner (such as sorting inside the window).

Best Practices for Implementing Sliding Window

  • Choose the Right Window Type: Establish early on whether fixed-size or variable-size windows are needed for the issue.
  • Track the State Efficiently: To keep track of frequencies or max/min values, use counters, hash maps, or deques.
  • Validate the edge cases: Test cases such as empty arrays, extremely small arrays, or values of k greater than n should always be used.
  • Incremental Debugging: To validate accuracy while coding, print intermediate window states.

Sliding Window in Streaming Systems

Sliding windows are vital to streaming systems as big data and real-time processing become more prevalent:
  1. Apache Kafka/ Apache Flink: Events are aggregated in real-time streams via sliding windows.
  2. Monitoring Systems: Track requests over rolling intervals to identify increases or decreases in server traffic.
  3. Fraud Detection: Unusual transaction activity over the past few years can be found with the help of sliding windows.

Sliding windows are used by streaming systems to allow fast decision-making without storing the complete dataset in memory.

Advanced Applications of Sliding Window Algorithm

The window sliding algorithm can be used in more complex situations than just simple ones:
  • Data streams: Using little memory to process massive amounts of real-time data.
  • Machine Learning Preprocessing: Making rolling statistics or moving average calculations.
  • Signal Processing: Using rolling windows to handle time-series data.
  • Bioinformatics: Pattern matching through DNA or protein sequence analysis.

These applications highlight how versatile the window sliding method is, going far beyond traditional data structures.

Real-world Applications of Sliding Window Technique

The window sliding method has essential real-world applications in a variety of industries and is not just restricted to algorithmic problems:

Finance and Stock Market Analysis

  • Moving Averages: Traders calculate simple moving averages (SMA) or exponential moving averages (EMA) over stock price data using window sliding methods.
  • Volatility Tracking: Windows of varying sizes can be useful for monitoring times when volatility is high.

Bioinformatics and Genomics

  • DNA Sequence Analysis: To look for motifs, repeats, or GC content in lengthy DNA sequences, sliding windows are used.
  • Protein matching: Helps in identifying similarities between subsequences of different proteins.

Recommendation Systems

  • User Activity Tracking: To make timely recommendations, sliding windows can keep an eye on users’ recent activities, such as the ten movies they have watched.
  • Session-based Behavior Modeling: Systems can adapt to changing session duration due to variable-size windows.

Time-series Forecasting

  • Sensor Data Analysis: Sliding windows are utilized to calculate rolling metrics in IoT devices, which often stream continuous data.
  • Detecting odd increases or decreases in performance metrics is known as anomaly detection.

Natural Language Processing (NLP)

  • N-grams: N-grams are extracted for language modeling using fixed-size sliding windows in natural language processing (NLP).
  • Entity Recognition: Contextual phrases related to words can be captured with the help of sliding windows.

Future Scope of Sliding Window Applications

The need for efficient algorithms, like the sliding window technique, will only grow as data continues to grow exponentially:
  • Edge Computing: For local analytics, devices with low memory will mainly depend on sliding windows.
  • AI and ML Pipelines: Contextual windows and rolling averages are vital preprocessing tools.
  • Cybersecurity: Variable-size windows sliding for anomaly monitoring will remain a feature of real-time threat detection systems.

Conclusion

In computer science, one of the most efficient and adaptable methods is the sliding window technique. The idea is always the same, whether the sliding window approach is used to solve conventional sliding window problems in arrays and strings or to guarantee reliable communication in computer networks: optimize by reusing earlier work as the windows shift.

Programmers and computer scientists can resolve a range of problems, from real-world system optimizations to competitive programming puzzles, by becoming proficient with data structures’ sliding windows.

Knowing and using the sliding window algorithm is critical in a world where efficiency is critical.

Megana Natarajan