Two Pointer Technique in Data Structures Explained

There are many clever methods in the field of algorithms that speed up and enhance memory efficiency when resolving issues. The two-pointer technique is one such tactic. It is possible that you have seen this method in action if you have run into issues with arrays, linked lists, or strings.

This blog will go into detail about the two-pointer approach, including what it is, why it works, how it differs from brute force, and how to use it for actual coding and interview problems. We will go over general trends, real-world examples, and possible dangers along the way.

Key Takeaways:
The two pointer technique in data structures uses two indices (or iterators) that traverse a structure in coordination to solve problems more efficiently than brute force. Variants include opposite direction, same direction, slow-fast pointers, and multi-array pointers, each suited to different problem types. This approach often reduces time complexity from \(O(n^2)\) to \(O(n)\) while using constant extra space (O(1)). Common problems where two pointers apply: two-sum in a sorted array, palindrome check, remove duplicates, detect cycle in linked lists, trapping rainwater, and merging sorted arrays. Key to correctness: clear pointer movement rules, proper boundary checks, and careful handling of edge cases (duplicates, nulls, pointer overlap). Two pointers are distinct from sliding window: sliding window targets contiguous subarrays with dynamic window sizing, while two pointers deal with relationships (pair sums, comparisons) often on sorted data. After mastering two pointers, you can progress to related techniques like sliding window, binary search, greedy methods, and dynamic programming to solve more complex challenges.

Key Takeaways:

The two pointer technique in data structures uses two indices (or iterators) that traverse a structure in coordination to solve problems more efficiently than brute force.
Variants include opposite direction, same direction, slow-fast pointers, and multi-array pointers, each suited to different problem types.
This approach often reduces time complexity from \(O(n^2)\) to \(O(n)\) while using constant extra space (O(1)).
Common problems where two pointers apply: two-sum in a sorted array, palindrome check, remove duplicates, detect cycle in linked lists, trapping rainwater, and merging sorted arrays.
Key to correctness: clear pointer movement rules, proper boundary checks, and careful handling of edge cases (duplicates, nulls, pointer overlap).
Two pointers are distinct from sliding window: sliding window targets contiguous subarrays with dynamic window sizing, while two pointers deal with relationships (pair sums, comparisons) often on sorted data.
After mastering two pointers, you can progress to related techniques like sliding window, binary search, greedy methods, and dynamic programming to solve more complex challenges.

What is the Two Pointer Approach?

In data structures, the two pointer technique is an algorithmic method that utilizes two indices, or pointers, to navigate a data structure in a coordinated manner. Two pointers, as opposed to traditional single pointer traversal, let you get rid of nested loops and solve issues more quickly.

Definition: Keep track of two variables (pointers) that relate to different locations inside a data structure.
Goal: Use these pointers wisely to achieve the issue’s goal without performing extra calculations.
Key Advantage: It usually reduces space complexity to (O(1)) and time complexity from (O(n^2)) to (O(n)).

Why Two Pointers Matter

Two Pointers shine when:

The input is sorted or has the possibility to be sorted.
You must locate ranges, subarrays, or pairs that satisfy specific requirements.
Naïve nested loops are what you wish to enhance.
The issue requires continuous additional space.

Variants of Two Pointer Technique

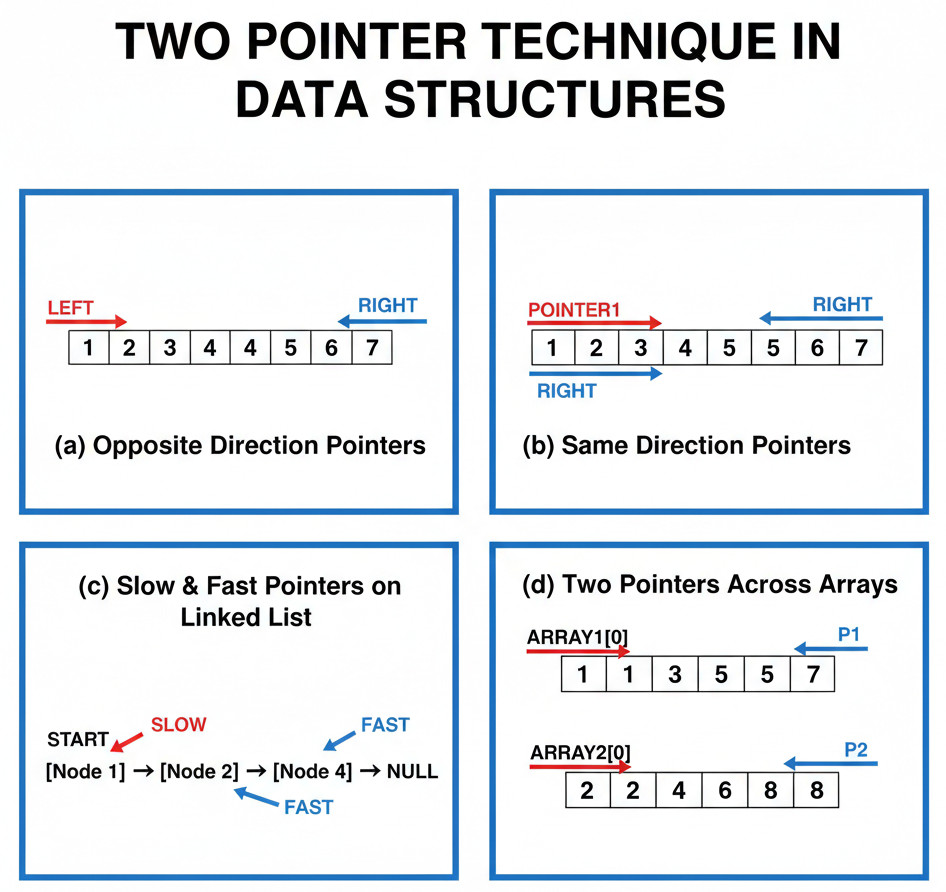
There is no one-size-fits-all solution for the two-pointer technique. You will choose a different variant based on the issue.

Opposite Direction Two Pointers

Setup: One pointer begins at the start, and the other at the finish.

Movement: Based on the scenarios, they move inward.

Use Cases:

Searching a sorted array for a pair with a target sum.
Validating whether a string is a palindrome.

Same Direction Two Pointers

Setup: Both guidelines start at the very beginning.

Movement: One pointer takes the lead, and the other follows.

Use Cases:

Eliminating duplicates from a sorted array.
Element comparison between two sorted arrays.

Slow and Fast Pointer Technique

Setup: One pointer takes one step, while the other takes a faster (often two-step) step.

Use Cases:

Floyd’s cycle detection algorithm for linked list cycle detection.
Locating a linked list’s middle element.
Validating linked lists’ palindrome characteristics.

Two Pointers on Multiple Arrays

Setup: Every pointer is placed on a different array.

Use Cases:

Combining two arrays that have been sorted.
Identifying shared components among arrays.

The Two Pointer Approach: How It Works

At its core, the technique exploits properties like sortedness or constraints to make decisions.

Set up pointers: Establish two indices.
Iterate: Relocate pointers as per the predetermined criteria.
Terminate: When the pointers cross or come to an end, stop.
Condition handling: Select which pointer to move based on comparisons.

Every element is processed just once due to this step-by-step procedure.

Complexity Analysis of Two Pointers

Time Complexity: Usually (O(n)), since each pointer moves at most (n) times.
Space Complexity: Since only indices are stored, there is (O(1)) additional space.

Compared to brute force ((O(n^2))), this is a drastic improvement.

Use Cases and Problems Solved with Two Pointers

Two Sum in Sorted Array

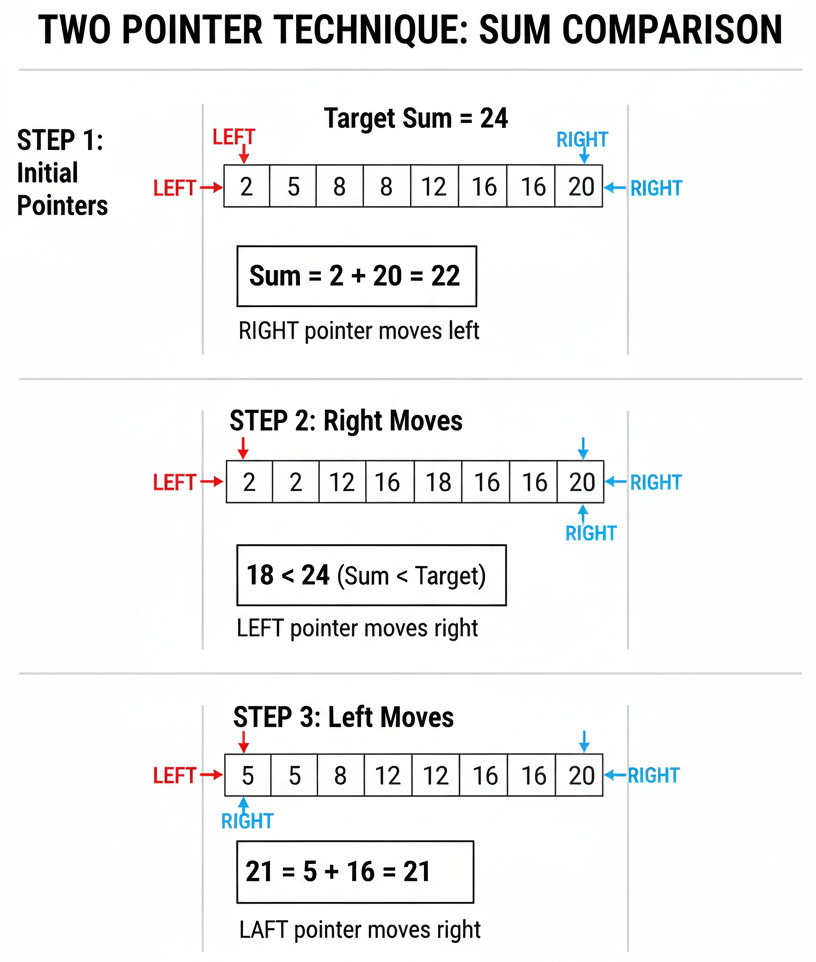
Use opposite pointers to find the pair given a sorted array and a target sum.
Move the left pointer if the sum is too small.
Move the right pointer if it is too large.
Stop when a pair is identified or pointers cross.

Palindrome Check in Strings

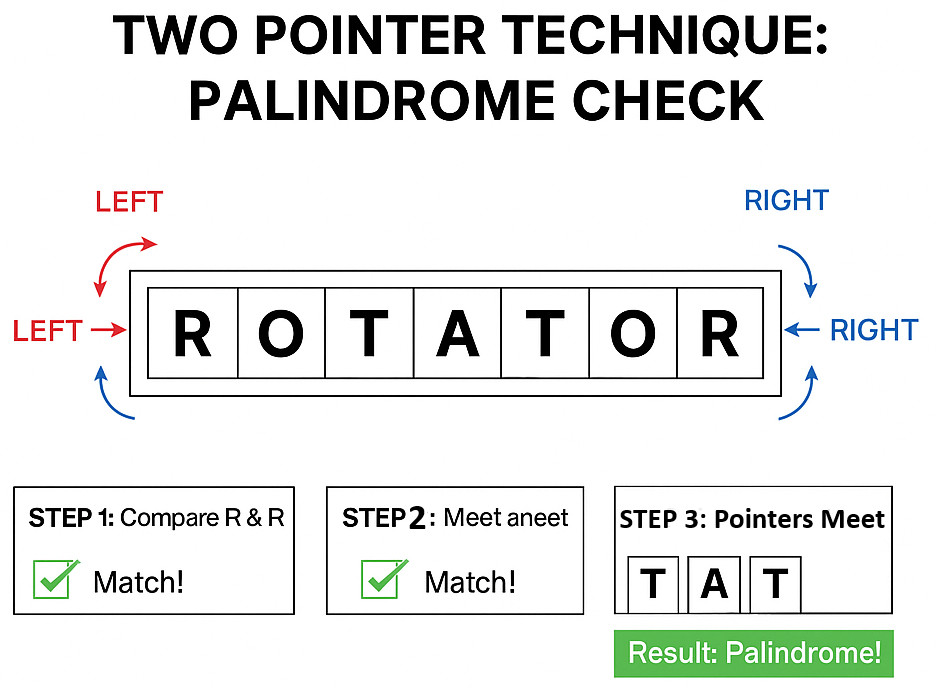
Compare the beginning and ending characters. Move inward if they match; if not, it isn’t a palindrome.

Remove Duplicates from the Sorted Array

For reading and writing distinct elements, use the same direction pointers.

Detect Cycles in Linked Lists

Use both fast and slow pointers. There is a cycle if they cross paths.

Container With Most Water (LeetCode Problem)

By shifting inward based on height comparisons, opposite pointers enhance area calculation.

Merging Two Sorted Arrays

It is more efficient to combine two pointers, one for each array, into a single sorted array.

Two Pointer Technique vs Sliding Window

The two sliding window and pointer methods are not the same, despite their similarities.

Two Pointers: Usually detected in sorted data, these pointers center on the relationships between elements.
Sliding Window: A dynamic window size solution for contiguous subarray problems.

For Example:

To find the “longest substring without repeating characters,” utilize a sliding window.
To “find two numbers that sum to target in a sorted array,” use two pointers.

Two Pointer Technique in Linked Lists

Linked lists bring unique applications of two pointers:

Middle Node: Slow moves one step, fast moves two. Slow is in the middle when fast reaches the end.
Cycle Detection: If a cycle is present, slow and fast pointers will meet.
Palindrome Check: Slow and fast aid in dividing the list and comparing its two halves.

Advanced Problems Using Two Pointers

Trapping Rain Water

When calculating trapped water, utilize opposite direction pointers to track the maximum left and right boundaries.

Subarray With Given Sum

Expand and contract a range utilizing the same direction pointers until the sum equals the expected amount.

Three Sum Problem

To find triples that meet the target, fix one element and then use opposite pointers on the remaining elements in the array.

Implementation Across Languages

The two pointer method is independent of language. Let us explore some code snippets and pseudocode in common languages.

Pseudocode for Two Sum (Sorted Array)

left = 0
right = n - 1
while left < right:
  sum = arr[left] + arr[right]
  if sum == target:
    return (left, right)
  else if sum < target:
    left++
  else:
    right--

Example Input: arr = [1, 2, 4, 7, 11, 15], target = 15

Output: (0-based indices) (0, 5) → values (1, 14) depending on dataset.

If arr = [2, 7, 11, 15], target = 9 → (0, 1) → values (2, 7).

Python Example

def two_sum(arr, target):
  left, right = 0, len(arr) - 1
  while left < right:
    s = arr[left] + arr[right]
    if s == target:
      return (arr[left], arr[right])
  elif s < target:
    left += 1
  else:
    right -= 1
  return None

Java Example

int[] twoSum(int[] arr, int target) {
  int left = 0, right = arr.length - 1;
  while (left < right) {
    int sum = arr[left] + arr[right];
  if (sum == target) return new int[]{arr[left], arr[right]};
  if (sum < target) left++;
  else right--;
}

return new int[]{};

C++ Example

pair<int,int> twoSum(vector<int>& arr, int target) {
  int left = 0, right = arr.size() - 1;
  while (left < right) {
    int sum = arr[left] + arr[right];
    if (sum == target) return {arr[left], arr[right]};
    if (sum < target) left++;
    else right--;
  }

  return {-1, -1};

}

Common Pitfalls and Mistakes

Ignoring the sorted requirement: Sorted arrays are assumed by many two-pointer solutions. Inaccurate results are obtained when the technique is applied to unsorted data without sorting.
Mismanagement of pointer overlap: Infinite loops or missed outcomes may be caused due to unclear stop conditions.
Inaccurate movement choices: Logical errors may occur from inadvertently moving the incorrect pointer when specific conditions are adhered to.
Disregarding duplicates: In issues like 3Sum or subset problems, failing to handle repeated values can arise from duplicate answers.
Null checks in linked lists: The program may crash if you overlook checking if fast.next or fast.next.next is null.
Negative numbers are ignored: In sum problems, overlooking negative values can lead to flawed pointer movement logic.
Overcomplicated solutions: Sometimes the simplest method is the most perfect one; if hashing or brute force is more practical, avoid forcing two pointers.
Ineffectively handling space trade-offs: Even though a hash map needs more space, there are scenarios in which it is cleaner. Consider trade-offs prior to resorting to two pointers.
Lack of testing: Only when tested on challenging datasets, such as all-negative arrays or extremely large arrays, do many logical errors become visible.

Interview Questions on Two Pointer Technique

Recruiters prefer to ask two pointer problems because it challenges algorithmic thinking:

Two sum in sorted array.
Remove duplicates from a sorted array.
Merge two sorted lists.
Detect a cycle in a linked list.
The container with the most water.
Trapping rainwater.
Valid palindrome check.

By practicing these, you can develop your intuition about when to utilize two pointers.

Comparing the Pointer Technique with Other Algorithms

Vs Brute Force: Nestled loops are broken by two pointers.
Vs Hashing: Two pointers often achieve (O(1)) space, whereas hash maps need (O(n)) space even though they can solve issues in (O(n)) time.
Vs Binary Search: Binary search solves search issues rather than pair/range issues.
Vs Divide and Conquer: Two pointers utilize linear sweeps rather than recursive splitting.

Real-World Applications of Two Pointer Technique

Two pointers have practical uses even though they are most often discussed in academic or interview contexts:

Text processing: In tasks related to natural language processing, such as comparing substrings or looking for palindromes.
Data cleaning: It is the process of eliminating duplicates or removing records that aren’t valid from sorted datasets.
Image processing: Verifying for symmetry by traversing pixel arrays from multiple ends.
Financial data analysis: Identifying transaction pairs that add up to a predetermined sum.

Two Pointer Technique in Competitive Programming

Two pointer issues occur frequently on competitive programming platforms such as LeetCode, Codeforces, and HackerRank. Learning this method can be advantageous:

Transform brute-force solutions into efficient algorithms.
Increase time efficiency when working with large input datasets.
Rapidly resolve issues such as 3Sum, Two Sum II, and Rainwater Trapping.

Visualization of Two Pointer Technique

For beginners, visualizing pointer movements helps build intuition:

Imagine a sliding ruler on a line of numbers that moves left or right based on whether the sum is too big or too small.
Alternatively, consider two people approaching one another from opposite ends of a street; they meet when the condition is met.
Visualization tools or dry-running code on paper are excellent ways to understand how pointers interact.

Best Practices For Using Two Pointers

Pay close attention to boundaries at all times: Ensure that you have the right loop conditions, which are usually while left <= right or while left <right. Off-by-one errors are common.
Use sorting as required: Sort first if the algorithm logic depends on ordering and the array isn’t sorted. Pay attention to the additional O(n log n) cost.
Clearly state the rules for movement: Select which condition moves the left and right pointers before you start coding. Clearly log this reasoning.
Handle duplicates gently: For certain problems (like 3Sum), it is necessary to skip duplicate values in order to avoid redundant results. Put this step into loops explicitly.
Test against edge cases: Try arrays of sizes 0, 1, or 2; arrays with all the same values; and maximum input sizes.
Give your variable names that are descriptive: To make code more self-explanatory, use left and right or slow and fast instead of just i and j.
Dry run with small inputs: Before scaling up, walk pointers through small arrays on paper or a whiteboard to validate logic.
Measure efficiency: To make sure you are improving, always compare your implementation to brute force.

Future Learning Paths Beyond Two Pointers

After mastering the two-pointer method, you can examine related algorithmic patterns:

Sliding Window: Ideal for issues involving subarrays or dynamic ranges.
Binary Search: When working with sorted arrays, it complements two pointers.
Greedy Algorithms: In order to optimize, greedy algorithms are occasionally combined with two pointers.
Dynamic Programming: Resolves overlapping subproblems by going beyond two pointers.

By building upon these two guidelines, you strengthen your algorithmic toolbox and get ready for challenges that get more complicated.

Conclusion: Mastering the Two Pointer Technique

In data structures, the two pointer technique is a flexible, innovative method that makes difficult issues easier to understand. Strong algorithmic problem solving is characterized by knowing when and how to apply two pointers, regardless of whether you are working with arrays, strings, or linked lists.

You can confidently manage typical interview questions and competitive programming challenges by being aware of their variations, use cases, and pitfalls. This method is a must-have in any developer’s toolbox, whether they are looking for pairs in arrays or identifying cycles in linked lists.

Megana Natarajan