Binary Indexed Tree in Data Structures Explained
One of the most potent and basic concepts in data structures is the tree. They aid effective searching, updating, and querying processes by helping us organize data hierarchically. The Fenwick Tree (also called the Binary Indexed Tree) and Segment Tree are two instances of specialized structures within the general category of trees that are made for range queries and cumulative computations. We will explore these structures, understand their underlying principles, and examine their relative efficiency.
| Key Takeaways: |
|---|
|
Why Binary Indexed Trees?
A basic data structure, arrays are often used to store elemental sequences. Arrays can be ineffective for regular updates or cumulative computations, even though they provide constant-time access to elements. Think about scenarios like maintaining frequency counts, figuring out the total sales over the first i days, or dynamically ranking elements as new information becomes available. Iterating over i elements is necessary when performing prefix sum queries naively, which leads to O(n) time complexity. While static prefix sums decrease query times to O(1), they are inefficient during updates because every change needs recalculating sums for all indices that follow.
In 1994, Peter Fenwick developed the Binary Indexed Tree (BIT), also known as a Fenwick Tree, as a way to efficiently handle cumulative frequency tables. By allowing both operations in O(log n) time, it reaches a balance between query and update efficiency. BIT helps with rapid value accumulation and updating without needing a complete structure rebuild by strategically storing partial sums and using the binary representation of indices.
- Online algorithms where data streams in and queries happen in real-time.
- Dynamic cumulative frequency tracking in text processing or telemetry data.
- Competitive programming challenges, like handling dynamic ranges, counting inversions, or maintaining order statistics.
Programmers working with dynamic numerical datasets, where queries and updates occur regularly, must understand BIT.
The Problem: Efficient Range Queries and Updates
- Determine the sum of the elements from index 1 to i in an array of size n.
- Modify an element’s value at a given index.
Each update might require recalculating prefix sums, which would take O(n) time, and each sum query would naively take O(n) time. When n and the number of queries are both high (such as millions of operations in financial systems or competitive programming), this becomes impractical.
Prefix sums could be considered: create an auxiliary array with prefix[i] = a[1] + a[2] +…+ a[i]. Prefix sum queries are therefore O(1). However, all prefix values from k onward must be recalculated if a single update takes place (for instance, modifying a[k]), which costs O(n). This poses a classic problem: how can we support quick updates as well as quick queries?
- O(log n) queries.
- O(log n) updates.
The trade-off is drastically better update efficiency than O(n), but queries are a little slower than O(1) prefix sums. These structures rely on the array being swiftly divided into blocks or segments.
Fenwick Tree (Binary Indexed Tree)
What is a Fenwick Tree?
The Binary Indexed Tree (BIT tree), sometimes referred to as the Fenwick Tree, is a specialized data structure made to efficiently manage prefix sums and updates.
Why is it called a Binary Indexed Tree?
Its strong dependence on binary representation of indices is where its name is derived from. The structure determines the range of data that each node (or element in the BIT array) represents by taking advantage of an index’s least significant bit (LSB). The tree can efficiently cover overlapping segments without explicitly storing them as a complete tree structure due to this binary manipulation.
Core Idea
Information about a range of elements in the original array is stored at each position in the BIT array. When querying, we can traverse upward (to parents) or downward (to children) using deft jumps that the LSB determines. With n being the array size, this ensures that no more than O(log n) steps are taken.
Binary Indexed Tree: Structure and Working
Because 1-based indexing is often used, a BIT is implemented as a one-dimensional array, typically of size n+1.
A segment of the original array’s cumulative sum is represented by each index in the BIT array.
BIT[i]represents a block of sizei & -i, where&is the bitwise AND.- Example: if i=12 (binary 1100), then i & -i = 4. Thus, BIT[12] represents the sum of 4 elements ending at index 12 in the original array.
Working
- Initialize
sum = 0. - While
i > 0:- Add
BIT[i]to the sum. - Move to parent:
i = i - (i & -i).
- Add
- Return sum.
- While
i <= n:- Add delta to
BIT[i]. - Move to next responsible index:
i = i + (i & -i).
- Add delta to
This dual traversal guarantees updates and queries are efficient, as each operation only traverses O(log n) levels.
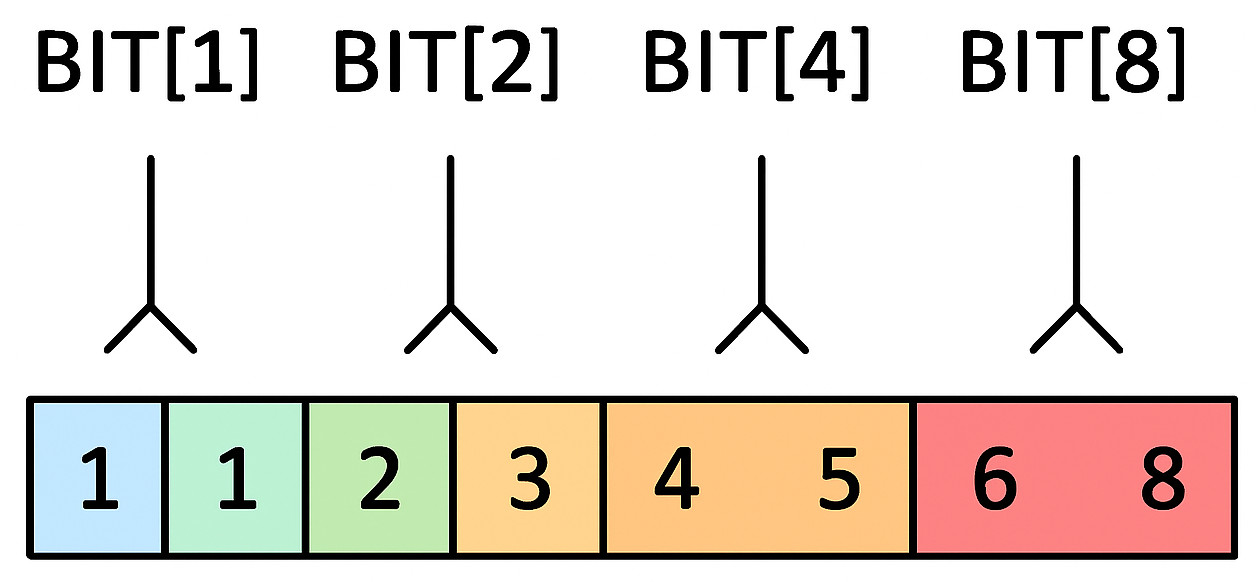
Fenwick Diagram
A Binary Indexed Tree splits an array into the overlapping segments, each of which is represented by an index in the BIT array, as shown in a Fenwick diagram. For example:
BIT[1] covers element 1.
BIT[2] covers elements 1-2.
BIT[4] covers elements 1-4.
BIT[8] covers elements 1-8.
These blocks come together to offer the necessary prefix sum when querying. It is easier to understand how ranges are effectively represented when this structure is visualized using a Fenwick diagram.
Advantages of Binary Indexed Tree
- Time Efficiency: Large data sets benefit from the fact that both update and query operations operate in O(log n).
- Space Efficiency: Just O(n) more space is required.
- Simplicity of Implementation: Less complicated to set up than segment trees. The operations mostly use bitwise index manipulation.
- Application in Competitive Programming: Because of its efficiency and simplicity, it is commonly utilized in prefix sum, frequency counting, and inversion counting problems.
- Dynamic Behavior: BIT enables the array to change dynamically through updates, in contrast to static prefix sums.
Limitations of Binary Indexed Tree
- Limited Range Query Support: Standard BIT does not directly support arbitrary range queries, but it does support prefix sums. Although range sums can be calculated using prefix(r) – prefix (1-1), other range operations, like minimum and maximum, are not natively supported.
- Non-Invertible Operations: Works best when used for invertible operations, like addition and subtraction. A BIT is not naturally compatible with operations such as min/max or GCD.
- Indexing Learning Curve: Beginners may find the dependence on binary manipulation (i & -i) frustrating.
- Extensions Needed for Range Updates: Highly complex modifications (such as the utilization of two BITs) are needed to accommodate both range updates and range queries, which makes it less simple.
Benefits of BIT (Binary Indexed Tree)
- More operations than just sums are supported, including min, max, GCD, LCM, and others.
- Using lazy propagation, it manages range and point updates.
- The segment tree, on the other hand, takes up to 4n memory and is more difficult to implement.
Segment Tree (Segment Tree GFG)
What is a Segment Tree?
Another tree-based structure is the segment tree, which is often covered in tutorials such as segment tree GFG, which explain how it is constructed recursively.
Structure
- A segment [1, r] of the array is represented by each node.
- The root covers [1, n].
- Every internal node divides into [1, mid] and [mid+1, r].
The results can be effectively aggregated across arbitrary ranges due to this recursive division.
- Build: It takes O(n) to build the tree. Every element is arranged in a leaf, and the sum, min, max, and other combined values are stored in internal nodes.
- Query: Navigate the tree and collate contributions from relevant nodes to establish the result in the range [L, R]. O(log n) is required for this.
- Update: When one element changes, update O(log n) nodes throughout the tree to reflect the change.
Segment Tree Structure
- The entire array is denoted by the root.
- The union of the intervals of its children is represented by each internal node.
- Root → [1, n]
- Left child → [1, mid]
- Right child → [mid+1, n]
This recursive division enables addressing queries by combining results from pertinent segments.
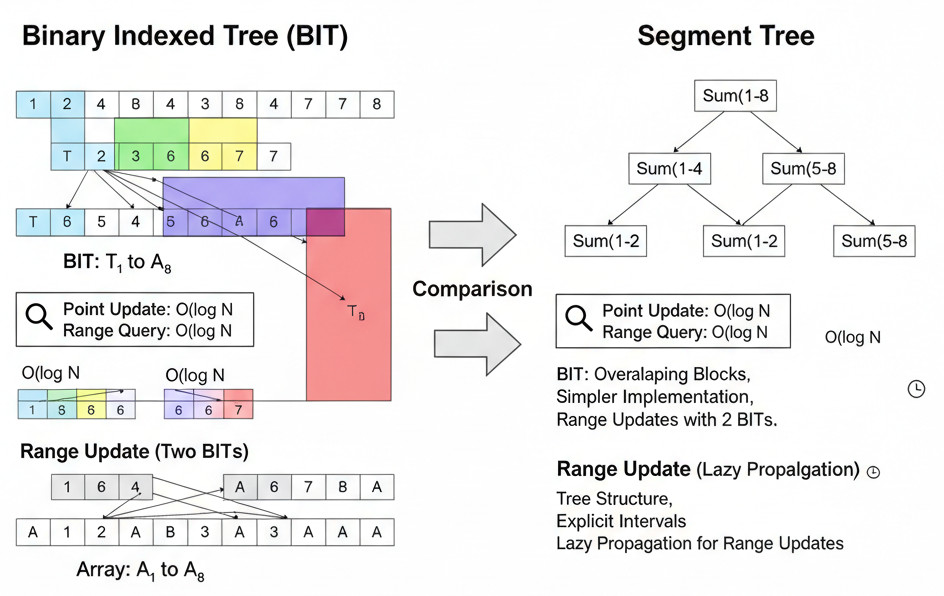
Binary Index Tree vs Segment Tree
| Feature | Binary Indexed Tree (Fenwick Tree) | Segment Tree |
|---|---|---|
| Supported Queries | Prefix sums, point updates | Range sums, min/max, range updates |
| Time Complexity | O(log n) | O(log n) |
| Space Complexity | O(n) | O(4n) |
| Ease of Implementation | Easier | More complex |
While the BIT tree is ideal for cumulative sums and inversion counting, the Segment Tree provides higher flexibility at the cost of complexity and memory.
Practical Applications
Binary Indexed Tree Applications
- Inversion Counting: Efficiently use a BIT to count the number of inversions in an array.
- Dynamic Frequency Tables: Helpful for cumulative frequencies or text compression (Fenwick’s original motivation).
- 2D Queries: In competitive programming, submatrix sum queries are expanded to two dimensions.
- Order Statistics: Use BIT to perform prefix sum searches in order to determine the k-th smallest element.
Segment Tree Applications
- Range Minimum/Maximum Queries (RMQ): Identify the minimum and maximum values in a subarray quickly.
- Lazy Propagation: Efficiently manage range updates, such as by adding a constant to a subarray.
- Advanced Aggregates: Provide support for custom associative functions, GCD, and XOR.
- Game Development and Physics Simulations: Interval handling and collision detection depend on range queries.
The core of efficient algorithms in domains ranging from databases and finance to machine learning and real-time systems is made up of BIT and segment trees.
Advanced Topics
Range Updates in BIT Tree
We can add range updates and range queries to a Binary Indexed Tree by keeping two BITs. In competitive programming, this tip is especially helpful.
2D Fenwick Tree
Grid submatrices can be queried using a 2D BIT. The idea is still the same: nested loops are required for updates and queries, and the indices are expanded into two dimensions.
Finding Index by Prefix Sum
A “binary lifting” technique can be used with Binary Indexed Trees to establish the largest index with a given prefix sum. In order-statistic problems, this is often utilized.
Choosing Between Binary Indexed Tree and Segment Tree
- Prefix sums and points are all that are needed.
- Memory is an issue.
- The goal is simplicity.
- You need more complex range queries (min, max, GCD, etc.)
- You need to update your range.
- Memory is not a big limitation.
Conclusion
The base of effective computer science problem-solving is made up of trees in data structures. Every structure, from basic binary trees to more complex ones like the Segment Tree and Fenwick Tree (Binary Indexed Tree), has advantages and uses. You can resolve a wide range of computational problems by understanding how these trees work through practice, Fenwick diagrams, and examples.
While the Segment Tree GFG approach provides a flexible and strong framework for more complicated range queries, the BIT tree is a simple and elegant solution for cumulative operations.
In actual use, the constraints of the problem and the kind of operations needed determine whether to use a Segment Tree or a Binary Indexed Tree. You will become a more proficient and adaptable programmer if you understand both.
|
|
