Deque in Data Structures: A Complete Guide
When programming using data structures, efficiency and flexibility are crucial. While commonly used data structures such as arrays, stacks, and queues provide a solid foundation, they sometimes lack versatility when it is needed. This is where a double-ended queue (Deque) comes in. A deque combines the properties of stacks and queues, with insertions and deletions taking place at both ends.
| Key Takeaways: |
|---|
|
This comprehensive guide to deques explores the concept in detail, including types of deques, common operations, implementation, applications, benefits, and limitations.
What is a Deque in Data Structures?
A Deque (pronounced as “deck”) stands for Double-Ended Queue and is a generalized version of stacks and queues that allows insertion and deletion of elements at the front and rear end of the queue.

- Insert elements at the front or rear.
- Delete elements from the front or rear.
- It acts like a stack (Last In First Out) when insertions and deletions occur at the same end.
- It behaves like a queue (First In, First Out) when insertions occur at one end and deletions at the other.
A typical deque looks as shown below:
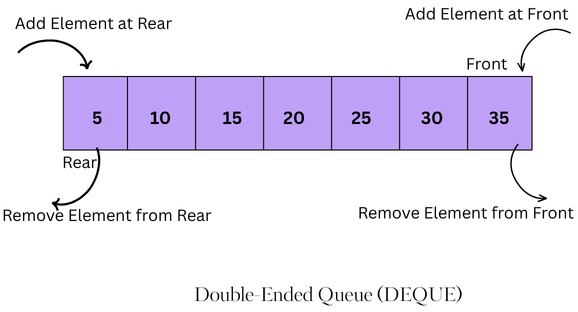
A deque is a generalized and versatile tool for various programming tasks, such as managing browser history, undo/redo functionality in editors, and scheduling algorithms where jobs are added and removed at both ends.
Key Characteristics of a Deque
- Generalized Queue: Deque is often considered a more generalized version of a queue, relaxing the strict FIFO principle.
- Linear Structure: Elements in a deque are arranged sequentially, so it is a linear structure.
- Dynamic Size: Deques can grow and shrink dynamically, unlike static arrays.
- Dual-Ended Operations: Deques support insertions and deletions from both the front (head) and rear (tail) of the data structure.
- Versatility: Deque supports both LIFO and FIFO operations.
- Efficient Access: Deque has constant-time, O(1), insertion and deletion operations in most implementations.
- Flexibility: It can be used to implement stacks and queues, combining the properties of both.
Types of Deque in Data Structures
-
Input-Restricted Deque
An input-restricted deque is one where deletion can be performed from both ends, but insertion can only be performed at one end.For an input-restricted queue, elements can be:- Inserted only at the rear end.
- Deleted from the front and rear ends.
-
Output-Restricted Deque
An output-restricted deque is one where insertion can be made at both ends, but deletion can only be made from one end.For an output-restricted queue, elements can be:- Deleted only at the front end.
- Inserted at the rear and front ends.
Basic Operations on Deque
-
Insertion Operations
-
insertFront(x): This operation adds an element to the front of the deque. The pseudocode for theinsertFrontoperation is as follows:1. Check the position of the front in the deque 2. If front < 1, reinitialize front to last index in the deque) 3. Then add a new element to the position pointed by the front deque[front] = x;
-
insertRear(x): An element x is inserted at the rear of the deque using theinsertRearoperation. The pseudocode for the same is given here:1. Check if the deque is full or not 2. If it's full, reinitialize rear = 0; else, increase rear by 1. 3. Then add the element to deque[rear]
-
-
Deletion Operations
-
deleteFront(): ThedeleteFront()operation removes the element from the front of the deque. Here is the pseudocode for this operation:1. Check if the deque is Empty. 2. If the deque is Empty, print the message “Deque Underflow” 3. If the deque has only one element, front = rear. 4. Delete element and set front =-1 and rear = -1 5. If the front is at the last index ( front == n-1 ), set front = 0. Else set Front = Front + 1. -
deleteRear(): ThedeleteRear()operation removes the element from the rear of the deque. The pseudocode for the operation is as follows.1. Check if the deque is Empty. 2. If the deque is Empty, print the message “Deque Underflow” 3. If the deque has only one element, front = rear. 4. If rear =0 , then set rear = n-1. Else rear = rear-1
-
-
Access Operations
getFront(): ThegetFront ()operation retrieves the front element of the deque without removing it.getRear(): To retrieve the rear element from the deque without removing it, thegetRear ()operation is used.
-
Utility Operations
isEmpty(): This operation checks if the deque is empty.
When the deque is empty, the front pointer is set to -1 (front = -1).isFull(): TheisFull ()function checks if the deque is full (in case of fixed-size implementation). The status of front and rear pointers in a full deque is:front == 0andrear == n-1ORfront == rear + 1, i.e., the two pointers cross over each other.
Implementation of Deque
Deques can be implemented using different underlying data structures:
1. Array Implementation
frontpointing to the first element.rearpointing to the last element.
Array implementation may also use circular arrays to utilize space efficiently.
Deques implemented using arrays have fast access. However, the size is predefined primarily, and resizing may be costly.
2. Linked List Implementation
A deque is implemented using a doubly linked list where each node contains data and pointers to previous and next nodes.
The advantage of this implementation is its dynamic size that grows and shrinks as needed without any resizing overhead.
However, extra memory is required to store pointers to previous and next nodes.
3. Using Libraries (in High-Level Languages)
- C++ STL:
deque<int> dq; - Java:
Deque<Integer> dq = new ArrayDeque<>(); - Python:
from collections import deque
4. Time Complexity of Operations
| Operation | Complexity |
|---|---|
| Insertion (front) | O(1) |
| Insertion (rear) | O(1) |
| Deletion (front) | O(1) |
| Deletion (rear) | O(1) |
| Access (front/rear) | O(1) |
Applications and Use Cases of Deque
- Palindrome Checker: A deque is used to check palindrome strings (strings that read the same forwards and backwards). String characters are inserted into a deque, and its front and rear elements are compared.
- Sliding Window Problems: It is used in sliding window problems, such as “maximum of all subarrays of size k,” where a deque efficiently maintains candidate elements.
- Job Scheduling: In job scheduling, tasks can be added or removed from both ends using a deque.
- Undo/Redo Functionality: Text editors and IDEs utilize deques to store actions and command history, including undo/redo.
- Memory Management: A deque is also used in managing memory, a pool of resources, and caching.
- Deque in Graph Algorithms: Traversal algorithms, such as 0-1 BFS, utilize a deque for shortest path problems with weights of 0 and 1.
- Browser History: Deque is used to manage browser history, enabling the implementation of back and forward features.
- Deque in Caching Algorithms: A deque is used in cache implementations, specifically in algorithms such as the Least Recently Used (LRU) algorithm, as it is efficient in removing old elements and adding new ones.
- Deque in OS Scheduling: Multi-level queue scheduling uses a deque to manage processes at different priorities.
- Deque in Simulation Systems: Deque is used to model waiting lines, call centers, and transport systems.
Advantages of Deque
- Deque is flexible as it supports both stack and queue operations and can therefore be used as either.
- Deque insertion and deletion at both ends are performed in constant time, providing efficiency.
- Deques support clockwise and anticlockwise rotations in O(1) time.
- Deques help solve complex real-time problems.
Limitations of Deque
- Similar to other data structure implementations, a fixed-size array implementation may lead to overflow.
- A linked list implementation of a deque requires extra memory for storing previous and next pointers.
- Random access is slower than arrays.
Example Implementations of Deque
#include <iostream>
using namespace std;
#define SIZE 10
class dequeue { //A deque class with operations
int a[SIZE], front, rear;
public:
dequeue();
void insert_at_beg(int);
void insert_at_end(int);
void delete_fr_front();
void delete_fr_rear();
void display();
};
dequeue::dequeue() {
front = -1;
rear = -1;
}
void dequeue::insert_at_end(int i) {
if (rear >= SIZE - 1) {
cout << "\nInsertion not possible, overflow!" << endl;
} else {
if (front == -1) {
front = 0;
}
rear++;
a[rear] = i;
cout << "\nInserted at end: " << a[rear] << endl;
}
}
void dequeue::insert_at_beg(int i) {
if (front == -1) {
front = 0;
rear = 0;
a[front] = i;
cout << "\nInserted at beginning: " << i << endl;
} else if (front > 0) {
front--;
a[front] = i;
cout << "\nInserted at beginning: " << i << endl;
} else {
cout << "\nInsertion at beginning not possible, overflow!" << endl;
}
}
void dequeue::delete_fr_front() {
if (front == -1) {
cout << "Deletion not possible: dequeue is empty" << endl;
} else {
cout << "Deleted from front: " << a[front] << endl;
if (front == rear) {
front = rear = -1;
} else {
front++;
}
}
}
void dequeue::delete_fr_rear() {
if (front == -1) {
cout << "Deletion not possible: dequeue is empty" << endl;
} else {
cout << "Deleted from rear: " << a[rear] << endl;
if (front == rear) {
front = rear = -1;
} else {
rear--;
}
}
}
void dequeue::display() {
if (front == -1) {
cout << "Dequeue is empty" << endl;
} else {
cout << "Dequeue elements: ";
for (int i = front; i <= rear; i++) {
cout << a[i] << " ";
}
cout << endl;
}
}
int main() {
dequeue d;
d.insert_at_end(2);
d.insert_at_end(4);
d.insert_at_beg(5);
d.insert_at_beg(6);
d.display();
d.delete_fr_front();
d.delete_fr_rear();
d.display();
d.insert_at_end(10);
d.insert_at_beg(1);
d.display();
d.delete_fr_front();
d.delete_fr_rear();
d.display();
return 0;
}
Inserted at end: 2 Inserted at end: 4 Insertion at the beginning not possible, overflow! Insertion at beginning not possible, overflow! Dequeue elements: 2 4 Deleted from front: 2 Deleted from rear: 4 Dequeue is empty Inserted at end: 10 Insertion at beginning not possible, overflow! Dequeue elements: 10 Deleted from front: 10 Deletion not possible: dequeue is empty Dequeue is empty
deque class from the Python collections library. The program executes all the primary functions of the deque class.
from collections import deque #use the deque from collections
# Create a deque
my_deque = deque()
# Add elements to the right (rear)
my_deque.append('a')
my_deque.append('e')
# Add elements to the left (front)
my_deque.appendleft('i')
print("Deque after Insertions:", my_deque)
# Remove elements from the right (rear)
removed_right = my_deque.pop()
print("Deleted from right:", removed_right)
print("Deque after pop():", my_deque)
# Remove elements from the left (front)
removed_left = my_deque.popleft()
print("Deleted from left:", removed_left)
print("Deque after popleft():", my_deque)
# Other useful methods
my_deque.extend(['o', 'u']) # Extend from the right
my_deque.extendleft(['m', 'g']) # Extend from the left
print("Deque after extend and extendleft:", my_deque)
my_deque.rotate(1) # Rotate elements to the right by 1 position
print("Deque after rotate(1):", my_deque)
my_deque.rotate(-1) # Rotate elements to the left by 1 position
print("Deque after rotate(-1):", my_deque)
my_deque.clear() # Remove all elements
print("Deque after clear():", my_deque) # Output: deque([])
Deque after Insertions: deque(['i', 'a', 'e']) Deleted from right: e Deque after pop(): deque(['i', 'a']) Deleted from left: i Deque after popleft(): deque(['a']) Deque after extend and extendleft: deque(['g', 'm', 'a', 'o', 'u']) Deque after rotate(1): deque(['u', 'g', 'm', 'a', 'o']) Deque after rotate(-1): deque(['g', 'm', 'a', 'o', 'u']) Deque after clear(): deque([])
Conclusion
A deque is a powerful and flexible data structure that extends the capabilities of stacks and queues. It is beneficial in solving complex algorithms, such as sliding window problems, graph traversals, and task scheduling, due to its constant-time operations.
Understanding deques not only helps you master data structures but also equips you with the tools to tackle real-world computing problems efficiently. Whether you implement it using arrays, linked lists, or built-in libraries, deques prove to be an indispensable part of programming and algorithm design.
|
|
