Prefix Sum Technique in Data Structures Explained

One of the most fundamental yet effective data structures and algorithmic strategies is the prefix sum technique. It is often used in real-world optimization problems, coding interviews, and competitive programming. This method reduces the complexity of repetitive queries and subarray problems from linear time to constant time by precalculating cumulative sums of an array. In-depth discussions of prefix sum arrays, the prefix sum algorithm, its applications, its benefits, comparisons with suffix sums and suffix arrays, and advanced variations and pitfalls will all be covered in this extensive blog.

Our emphasis will be on depth and clarity, so this blog will be a dependable resource whether you are unfamiliar with the idea or wish to brush up on your understanding.

What is Prefix Sum?

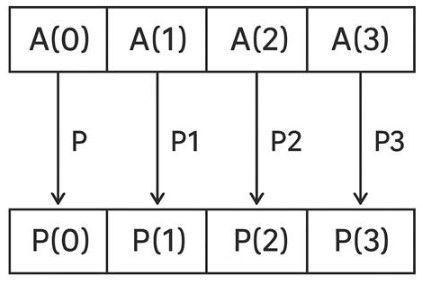
Let us start by addressing the most fundamental query, what is the prefix sum?

The running total of array elements up to a specified index is the fundamental definition of a prefix sum. The prefix sum array P is defined as follows for an array A of length n:

[P[i] = A[0] + A[1] + A[2] +… + A[i]]

To put it in simpler manner, every element in the prefix sum array is the sum of every element in the original array up to that index. The computational benefits of this minor change are enormous. Why is this important? Rather than repeatedly iterating through the subarray’s elements, we can use the below to calculate the sum of any subarray:

[Sum(l, r) = P[r] – P[l-1]]

This is efficient because subtracting the prefix up to l-1 eliminates all elements before l, whereas the prefix sum up to index r includes everything from the beginning to r. The sum is simply P[r] in the special case where l = 0.

When responding to multiple queries, this formula becomes necessary because it converts what would usually take O(n) per query into a constant-time operation.

Building the Prefix Sum Array

Prefix Sum Algorithm

The prefix sum algorithm constructs the prefix sum array in one pass:

1. Create an array P of the same size as A.
2. Initialize P[0] = A[0].
3. For each index i from 1 to n-1, do:
4. P[i] = P[i-1] + A[i]

This is a linear-time preprocessing step (O(n)) that allows extremely fast queries.

Example Walkthrough

Consider the array:

A = [3, 1, 4, 1, 5, 9]

The prefix sum array is:

P = [3, 4, 8, 9, 14, 23]

• The sum of elements from index 2 to 4 (i.e., [4, 1, 5]) is:

P[4] – P[1] = 14 – 4 = 10

This took a constant-time subtraction instead of iterating through three elements.

Implementation Complexity

• Time Complexity (preprocessing): O(n)
• Query Complexity: O(1)
• Space Complexity: O(n)

This compromise of extra memory for faster queries is a signature of prefix sum usage.

Why Prefix Sums Are Useful

The prefix sum drastically changes our approach to range based and goes beyond simply adding numbers together. This is the reason it is so important:

Speeding Up Range Queries:

Generally, we would loop through each element in that subarray to identify the sum of element from index l to r, which takes O(r-l+1) time. We preprocess once in O(n) when utilizing prefix sums, and each subsequent query is O(1). This is transformative for big datasets with loads of queries.

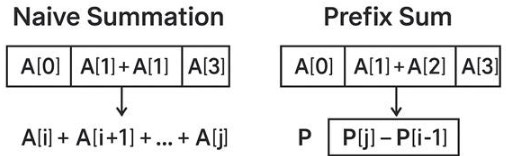
Handling Multiple Queries Efficiently:

Imagine being delegated with calculating the sum of one million unique subarrays in a sizable dataset. This would be computationally impossible without prefix sums. The preprocessing step allows instantaneous answers to all queries using prefix sums.

Generalization Beyond Sums:

While prefix sums are most often used for sums, they can also be used for counts, XORs, products, and other accumulative attributes. For example, quick range XOR queries, which are often used in bitwise problems, are made possible by a prefix XOR array.

Memory vs. Time Tradeoff:

We could prevent billions of unnecessary computations by storing an extra O(n) array. In most scenarios, this trade-off is acceptable, especially in programming competitions with tight deadlines.

Building Block for Advanced Algorithms:

More complex data structures like Segment Trees and Fenwick Tree are supported by prefix sums. It is much easier to learn those concepts if you understand prefix sums.

Applications of Prefix Sum Algorithm

Prefix sums appear in many different contexts. Let’s explain more on the primary uses:

Range Sum Queries

• The most popular use case. With prefix sums, Sum(I, r) is computed as P[r]- P[l – 1].
• Example: Swiftly determine the total price movement over two days in a stock price array.

Counting Properties in Ranges

• To keep track of counts of a property, like “number of even numbers up to index i” or “frequency of a particular character in a string,” create a prefix array.
• Example: In DNA sequencing, preprocess the number of “A,” “C,”” G,” and “T”s that occur up to each index before responding immediately to any frequency query.

Subarray Problems

• Prefix sum plus hashing are utilized to resolve issues like “how many subarrays sum to K’ and “longest subarray with sum = K.”
• Example: Store seen prefix sums in a hashmap and use it to swiftly determine whether currentPrefix – K exists.

Equilibrium Index / Pivot Index

• These indices divide an array so that the sums on the left and right are equal. Checking this at each index becomes O(1) when prefix sums are used.

2D and Matrix Issues

• For rectangular queries in grids or images, extend prefix sums to two dimensions.
• Example: Utilize a sum-area table to quickly determine the total brightness in a rectangular area of a grayscale image.

Sliding Window Optimizations

When queries overlap, prefix sums can occasionally take the place of sliding windows, enabling for O(1) retrieval without re-traversal.

Prefix Sums vs Suffix Arrays

• Prefix Sum Array: Stores starting cumulative sums.
• Suffix Sum Array: Similar, but starting at the end of the array.
• Suffix Array (string data structure): Totally different, used in text processing, it stores a string’s sorted suffixes for substring searches.

Prefix sums and suffix sums are generally the relevant contrast for data structure problems.

Example of Suffix Sum Array

A = [2, 4, 6]

Suffix Sum = [12, 10, 6].

When assessing right-hand-side total, specially in equilibrium or partitioning problems, this is helpful.

Common Problems Solved Using Prefix Sums

1. Equilibrium Index:
   • Given [-7, 1, 5, 2, -4, 3, 0], the equilibrium index is 3 because -7+1+5=-1 and -4+3+0=-1. Prefix sums make this check O(n).
2. Split Array into Two Equal Sums:
   • Use total sum S. If there exists an index i such that P[i] = S/2, then the array can be split at i.
3. Count Subarrays with Sum = K:
   • Maintain a hashmap: map[prefixSum] = frequency. At each step, check if prefixSum – K exists in the map. This turns a naive O(n²) solution into O(n).
4. Longest Subarray with Sum = K:
   • Store the earliest index where a prefix sum occurs. If prefixSum – K reappears later, the subarray between them has sum = K, and its length can be tracked.
5. Subarray Sum Divisible by K:
   • Use prefix sums modulo K. If two prefix sums leave the same remainder, the subarray between them is divisible by K.
6. 2D Range Queries:
   • In a grid of rainfall values, a 2D prefix sum can immediately tell you the rainfall total in any rectangular region, from city blocks to satellite images.

Prefix Sum in Competitive Programming

• Time Efficiency: When brute force is used to resolve a problem, it often takes thousands of queries.
• Versatility: They work equally well in 1D and 2D and can be applied to sums, counts, and XORs.
• Low complexity: Simpler to put in practice on a short notice.
• Integration with Hash Maps: A common pattern in medium-to-hard problems is the combination of prefix sums and hashing.
• Matrix-based Problems: 2D prefix sums are a popular tool among content setters for grid problems such as matrix-based DP problems, game boards, and image analysis.

Preprocessing prefix sums and then responding to all queries in O(1) reduces O(n*q) solutions to O(n+q), which is a common competitive programming method.

Implementation Details and Pitfalls

Developers often commit minor errors when working with prefix sums. Important dangers include:

Indexing Errors:

• The most common problem is the confusion between zero-based and one-based indexing.
• The best practice is to use P[0] = 0 to create a prefix array of size n+1. Consequently, P[r+1] – P[1] = Sum (1,r).

Edge Cases:

• Care must be exercised when handling queries that begin at index 0.

Negative Numbers:

• Works well, but use caution when combining hash maps with prefix sums (make sure negative keys are handled correctly).

Integer Overflow:

• Prefix sums of big arrays may be greater than 32-bit integers in languages like Java or C++. Make use of 64-bit integers (long long in C++).

Dynamic Updates:

• Prefix sums don’t change. You will need to recalculate if the underlying array changes frequently. Segment trees or Fenwick trees work better in these situations.

Advanced Variants

There are multiple effective extensions and variations of the prefix sum technique:

Difference Array:

• Allows O(1) range updates. To gain the final values, calculate the prefix sum of the difference array after processing all updates.
• Example: In O(1), increment all elements between indices 1 and r by +5.

Prefix XOR Array:

• Helpful for bitwise operation problems. Range XOR can be found as PX[r]^PXX[l-1] because XOR is invertible.
• Example: Validate if the subarray’s XOR equals the desired value.

Prefix Product Array:

• Stores accumulated goods. Be aware that division is not always valid because it can be broken by zero elements. Often applied to problems like “product of array except self.”

Multidimensional Prefix Sums:

• Graphics, games, and DP often use 2D prefix sums (summed-area tables) and even 3D extensions.
• Example: Swiftly calculate the population in any rectangular area of a city grid.

Modular Prefix Sums:

• For divisibility or cycle detection, we are often interested in sums modulo K. Several problems are simplified by prefix sums modulo K.

Hybrid Structures:

• Prefix sums work well in hybrid solutions for complex problems when paired with sliding windows, hashing, or binary search.

In short, one of the most simple and adaptable data structure techniques is the prefix sum technique. We can preprocess cumulative sums and convert expensive operations into constant time queries by building a prefix sum array. Range queries, subarray problems, averages, equilibrium checks, and multidimensional queries can all benefit from it.

Conclusion

Prefix sums function as an example of how a simple concept can serve as the foundation for algorithmic problem-solving. They offer a starting point for learning more complex structures like segment trees and strike a balance between efficiency and preprocessing. One of the most sophisticated and useful data structures tools is the prefix sum technique, which can be applied to arrays, matrices, sums, or XOR.

Once you get the hang of it, you will resolve problems more confidently and efficiently.

Megana Natarajan