Queue in Data Structures: A Complete Guide with Types, Operations & Examples
Data structures enable efficient data storage, retrieval, and manipulation, and form the backbone of computer science. Apart from arrays, linked lists, and stacks, a queue is a linear data structure that models a real-world waiting line.
| Key Takeaways |
|---|
|
This article provides a comprehensive guide to queues in data structures, exploring their characteristics, types, operations, implementations, and real-world applications. It is followed by an analysis of their advantages and limitations.
What is a Queue in Data Structures?
A queue is a linear data structure that follows the First In First Out (FIFO) principle, so the first element inserted is the first to be popped out.
It is similar to people standing in line at a ticket or billing counter, or at a bus stop to board the bus. So, when you see people queuing up anywhere, it is a real-time example of a queue. In a queue, the person standing at the front of the queue (the First person) is the one who gets to leave the queue first.
Similarly, if anyone wants to join the queue, they must participate at the rear end.

Key Characteristics
- Queues are linear data structures in which their elements are arranged sequentially.
- Queues use FIFO access, which means the first element added to the queue is the first element to be removed.
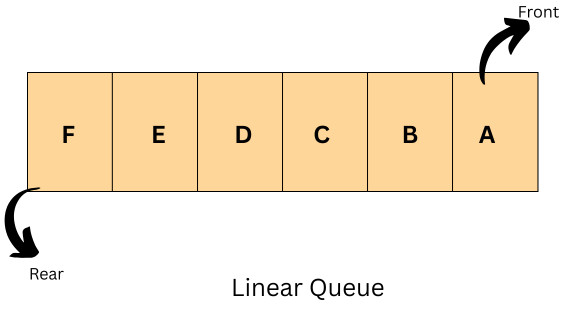
- A queue has two pointers, namely, the front of the queue and the rear of the queue.
- Front: This pointer points to the front of the queue. This is the point at which elements are removed from the queue.
- Rear: This is the position at the end of the queue. The elements are added to the queue from the rear end.
A linear queue with its pointers is shown below:
FIFO Principle in a Queue
The FIFO (First In First Out) principle states that the first element added to the queue will be the first element removed from the queue.
Let us understand this with a real-life example.
Suppose you imagine a ticket counter where the number of people is interested in buying movie tickets. Naturally, they make a line in front of the counter. If you can imagine this line, the first person standing in this line will get the ticket first and leave the queue. As more and more people come to buy tickets, they will stand at the end of the line and not break it to join in between.
Hence, in programming terms, this line represents a queue with two ends: the front and the rear. Elements are added to the queue at the rear while they are removed from the queue at the front. According to the FIFO principle, the first element in the queue is removed first.
Basic Queue Operations in Programming
A queue supports the following set of standard operations:
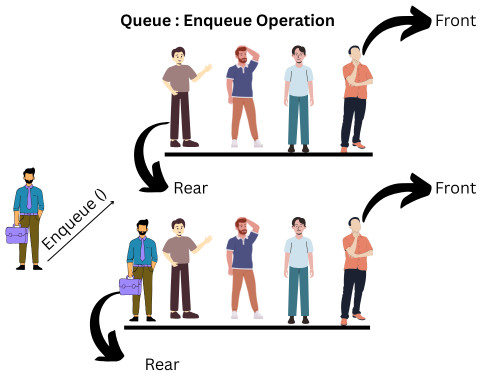
Enqueue(x)
The Enqueue operation inserts an element into the queue. The element is always added at the rear of the queue, so it is appended to the end of the current queue items.
Enqueue () operation succeeds if the current queue is not full; otherwise, it prints the “Queue Overflow” message.
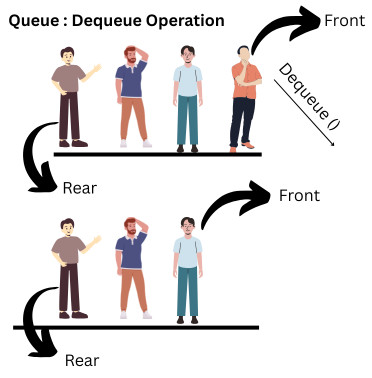
Dequeue()
This operation removes an element from the queue. The function removes the first element from the queue and returns it. If the queue is not empty, this function removes the element from the front of the queue; otherwise, it prints the “Queue Underflow” message.
Peek()/Front()
These functions do not modify the queue. Both peek () and front () return the element at the front (first element in the queue) without removing it.
isEmpty()
This is a Boolean function that checks if the queue is empty. If a queue is empty, this function returns ‘true’; else it returns ‘false’.
isFull()
Yet another Boolean function that checks if the queue has reached its maximum capacity (in case of array-based implementation).
Implementation of Queues
Similar to a stack data structure, queues can be implemented using arrays or linked lists, each with its own advantages and disadvantages.
1. Array Implementation
In the array implementation of queues, a queue data structure is represented as a fixed-size array. Two indices, front and rear, are defined to track the front and rear of the queue, respectively.
Initially, when the queue is empty, both indices are at the starting position. When an element is inserted into the queue, the rear index is incremented by 1(Enqueue). When an element is deleted from the queue, the front index is incremented by 1(Dequeue).
Although it is easy to implement queues using arrays, there is a significant drawback. After multiple dequeues, empty slots appear at the start of the array. However, these slots remain unused unless elements are shifted or a circular array is used.
Pseudocode:
Function Enqueue()
If Rear = MAXSIZE -1:
Return “Queue Overflow Error”
ElseIF (Front = -1 and Rear = -1):
Set Front = Rear = 0
Else
Set Rear = Rear + 1
End if
Set Queue[Rear} = NUM
End Enqueue()
Function Dequeue()
If Rear == -1 && Front == -1:
Return “Queue Underflow Error”
Else
Set Rem = Queue[Front]
Set Front = Front +1
End IF
End Dequeue()
Time Complexity:
- Enqueue: O(1) (if not full)
- Dequeue: O(1)
2. Linked List Implementation
When a queue is implemented using a linked list, each element in the queue is represented as a linked list node. Each node has a data part and a pointer to the next node. In this implementation as well, the two pointers, front and rear, are maintained and updated appropriately on dequeue and enqueue operations, respectively.
In this implementation, as a linked list is used to represent a queue, there is no maximum size limit. The size of the queue is allocated dynamically, and space is not wasted as in an array implementation.
Pseudocode:
FUNCTION Enqueue(Queue q, DATA item):
CREATE new_node AS Node
new_node.value = item
new_node.next = NULL
IF IsEmpty(q) THEN
q.front = new_node
q.rear = new_node
ELSE
q.rear.next = new_node
q.rear = new_node
FUNCTION Dequeue(Queue q) RETURNS DATA:
IF IsEmpty(q) THEN
PRINT "Queue Underflow"
RETURN ERROR_VALUE
ELSE
DATA removed_item = q.front.value
POINTER temp = q.front
q.front = q.front.next
IF q.front IS NULL THEN
q.rear = NULL
END IF
RETURN removed_item
Time Complexity:
- Enqueue: O(1)
- Dequeue: O(1)
Types of Queues in DSA
Based on the structure and functionality they offer, queues have several variations as follows:

1. Simple Queue (Linear Queue)
This is the simplest type of linear queue. It follows the FIFO principles and can be implemented using either arrays or a linked list.
A typical example of a linear queue is a ticket counter where people queue up to book tickets. The first person in the queue at the front is the first to get tickets and leave the queue.
The linear queue is easy to implement and maintain. However, when it is implemented using arrays, there is a wastage of space due to shifting.
2. Circular Queue
A circular queue is a queue data structure that treats the array as a circular structure. It uses a single, fixed-size buffer, as if it were connected end-to-end, forming a circle. A circular queue is a combination of a circular queue and a dequeue. It supports insertion and deletion of elements from both ends in a circular manner.
The circular queue has a fixed maximum size and is an efficient implementation for a queue. No shifting is needed, and the entire queue can be used to store elements.
A circular queue is primarily valuable for buffering applications, such as CPU scheduling.
3. Double-Ended Queue (Deque)
A deque is an extension of a standard queue in which insertion and deletion can be done from both ends, unlike in standard queues.
- Input-restricted deque: In this, insertion is allowed only at one end, while deletion can be done from both ends.
- Output-restricted deque: In this type of queue, deletion is allowed only at one end.
Deque is used in palindrome checking or sliding window problems.
4. Priority Queue
This is a linear queue with a difference that each element in the queue has a priority. The priority of the element determines which are to be deleted and processed first. Assigning priorities to elements can be based on various criteria.
An element with the highest priority is processed first. If there are two elements with the same priority, then the order of insertion of the element is considered.
A priority queue can be implemented using either arrays or linked lists. However, the binary heap implementation of priority queues is most efficient.
A priority queue is used in job scheduling within operating systems and for handling network packets.
Applications of Queue in Real Life
The following are some of the notable applications of the queue:
CPU Scheduling
Queues are excellent structures for managing processes of operating systems. Operating systems use queues to manage processes and determine which process will use the CPU next, often in a round-robin fashion.
Printer Queue
Jobs to be printed are lined up to be picked by the printer, following FIFO order. Multiple users send documents to the printer. A queue holds these print jobs and processes them one at a time, preventing conflicts.
Networking
Routers in networking that route packets use queues to manage packet forwarding. This way, the flow of data can be controlled and a decision made about transmitting or discarding a packet.
Breadth-First Search (BFS)
Algorithms used to traverse a graph, like BFS, rely on queues to explore nodes level by level. Using queues ensures that nodes are visited in the order of their distance from the starting node.
Call Centers / Ticket Systems
Customer requests in call centers or other counters are serviced in the order they arrive. Banks, ticket counters, call centers, and other service centers use queues to manage various requests as they arrive, in the order they are received.
Traffic Management
At toll booths and for traffic lights, queue mechanisms come in handy in managing the flow of vehicles, ensuring orderly and safe passage through complex intersections.
Queue vs Stack in Data Structures
Although queues and stacks are both linear data structures, their functionality and structure differ. The following table summarizes the key differences between a queue and a stack:
| Feature | Queue | Stack |
|---|---|---|
| Definition | A linear data structure that follows the First In First Out (FIFO) principle. | A linear data structure that follows the Last In First Out (LIFO) principle. |
| Primary Operations | Enqueue (add an item), Dequeue (remove an item), Peek/Front (view the first item) | Push (add an item), Pop (remove an item), Peek (view the top item) |
| Insertion/Deletion | Elements are added at the rear and removed from the front. | Elements are added and removed from the same end (the top). |
| Pointers | Two pointers (front and rear) are needed for queue operations. | Uses a single pointer called the top of the stack. |
| Complexity (Amortized) | Enqueue: O(1), Dequeue: O(1), Front: O(1), Rear: O(1) | Push: O(1), Pop: O(1), Peek: O(1) |
| Memory Structure | Typically uses a circular buffer or linked list. | Typically uses a contiguous block of memory or a linked list. |
| Implementation | Can be implemented using arrays, linked lists, or circular buffers. | Can be implemented using arrays or linked lists. |
| Use Cases | Function call management (call stack), expression evaluation, syntax parsing, and undo mechanisms in text editors. | Scheduling processes in operating systems, managing requests in a printer queue, and breadth-first search in graphs. |
| Real-World Analogy | A queue at a ticket counter: the first person in line is the first to be served. | A stack of plates: you add and remove plates from the top. |
Advantages of Queues
- FIFO Principle: Queues strictly follow the FIFO principle, ensuring that the first elements inserted into the queue are the first ones to be removed, thereby helping applications in a fair and predictable manner.
- Efficient Data Management: Queues excel at managing large datasets and processing them in an orderly fashion.
- Simple Implementation: They are relatively easy to understand and implement, making them suitable for novice programmers.
- Buffering and Resource Management: Queues support buffering, which is beneficial for asynchronous data transfers and managing system resources, such as CPU time, memory, and I/O devices.
- Fairness: The FIFO nature ensures that all items are processed without bias, leading to fair resource allocation and service delivery.
Limitations of Queues
- Limited Flexibility: Queue elements cannot be accessed randomly, as the access is strictly restricted to the two ends, front and rear.
- Time-Consuming Searches: Searching for a specific element within a queue is inefficient and time-consuming, as it often requires traversing the entire queue.
- Potential Memory Wastage: In a static, array-based implementation of queues, memory may be wasted because space used by deleted elements at the front cannot be reused once it is lost.
- “First-Come, First-Serve” Dilemma: In some real-world scenarios, the strict FIFO approach can lead to delays for new arrivals while long-waiting customers are still being served.
Queue in Different Programming Languages
Let us demonstrate the implementation of queues in C++ and Python:
Using C++
#include <iostream>
struct Node { //Node for queue element
int data;
Node* next;
Node(int val) : data(val), next(nullptr) {}
};
class LinkedListQueue {
private:
Node* front; //pointer to front of the queue
Node* rear; //pointer to rear of the queue
public:
LinkedListQueue() : front(nullptr), rear(nullptr) {}
bool isEmpty() { //check if queue is empty
return front == nullptr;
}
void enqueue(int value) { //insert element into the queue
Node* newNode = new Node(value);
if (isEmpty()) {
front = newNode;
rear = newNode;
} else {
rear->next = newNode;
rear = newNode;
}
std::cout << value << " enqueued." << std::endl;
}
int dequeue() { //remove element from the queue
if (isEmpty()) {
std::cout << "Queue is empty. Cannot dequeue." <<
std::endl;
return -1;
}
int dequeuedValue = front->data;
Node* temp = front;
front = front->next;
if (front == nullptr) { // If queue becomes empty
rear = nullptr;
}
delete temp;
std::cout << dequeuedValue << " dequeued." <<
std::endl;
return dequeuedValue;
}
int getFront() { //peek operation
if (isEmpty()) {
std::cout << "Queue is empty." << std::endl;
return -1;
}
return front->data;
}
void display() const { //display queue contents
if (front == nullptr) { // Queue is empty
std::cout << "Queue is empty" << std::endl;
return;
}
Node* temp = front;
while (temp != nullptr) {
std::cout << temp->data << " ";
temp = temp->next;
}
std::cout << std::endl;
}
};
int main() {
LinkedListQueue q;
q.enqueue(10);
q.enqueue(20);
q.enqueue(30);
std::cout<<"Queue: ";
q.display();
std::cout << "Front element: " << q.getFront()<< std::endl;
q.dequeue();
std::cout<<"Queue after dequeue operation: ";
q.display();
std::cout << "Front element: " << q.getFront()<< std::endl;
return 0;
}
10 enqueued. 20 enqueued. 30 enqueued. Queue: 10 20 30 Front element: 10 10 dequeued. Queue after dequeue operation: 20 30 Front element: 20
Using Python
class Queue: #class queue
def __init__(self):
self.queue = []
def enqueue(self, element):
self.queue.append(element)
def dequeue(self):
if self.isEmpty():
return "Queue is empty"
return self.queue.pop(0)
def peek(self):
if self.isEmpty():
return "Queue is empty"
return self.queue[0]
def isEmpty(self):
return len(self.queue) == 0
def size(self):
return len(self.queue)
# Create a queue
myQueue = Queue()
myQueue.enqueue('P')
myQueue.enqueue('Y')
myQueue.enqueue('T')
myQueue.enqueue('H')
myQueue.enqueue('O')
myQueue.enqueue('N')
print("Original Queue: ", myQueue.queue)
print("Front of the Queue: ", myQueue.peek())
print("Dequeue: ", myQueue.dequeue())
print("Queue after Dequeue: ", myQueue.queue)
print("Front of the Queue: ", myQueue.peek())
print("isEmpty: ", myQueue.isEmpty())
print("Size: ", myQueue.size())
Original Queue: ['P', 'Y', 'T', 'H', 'O', 'N'] Front of the Queue: P Dequeue: P Queue after Dequeue: ['Y', 'T', 'H', 'O', 'N'] Front of the Queue: Y isEmpty: False Size: 5
Time and Space Complexity Analysis
The following table shows the complexity for basic queue operations for array and linked list implementations:
| Operation | Array Implementation | Linked List Implementation |
|---|---|---|
| Enqueue | O(1) (amortized) | O(1) |
| Dequeue | O(1) | O(1) |
| Peek | O(1) | O(1) |
| Space | O(n) | O(n) |
Future of Queues in Computer Science
Computer systems are continually evolving and are becoming increasingly distributed and real-time. With this evolution, queues will remain a relevant concept. Newer technologies, such as Kafka, RabbitMQ, and Amazon SQS, are built on the idea of message queues and enable scalable and fault-tolerant systems.
Queues will also continue to play a critical role in communications, buffering, and workload distribution with the rise of event-driven architectures and microservices.
Conclusion
A queue is a fundamental, linear data structure that models real-world scenarios and underpins numerous algorithms and systems. They provide powerful tools for scheduling, buffering, and process management.
By understanding queues, their types, operations, and implementation in various languages, as well as their real-world applications, developers can utilize queues more effectively to design efficient, fair, and reliable systems.
|
|
