Stack in Data Structures: A Complete Guide with Operations & Examples
Data structures are fundamental in creating efficient algorithms and optimizing system performance in computer science and programming. They form the backbone of efficient algorithms and program design. Among these data structures, the stack data structure stands out due to its simplicity and effectiveness.
| Key Takeaways: |
|---|
|
This comprehensive guide on stack data structure will explore the stack, its operations, representation, implementation, and real-world applications.
What is a Stack in Data Structures?
A stack is a linear data structure that follows a specific order for operations, commonly called Last-In-First-Out (LIFO). This means the last element added to the stack is the first one to be removed.

The stack is a data structure designed in such a way that you can only access the element that is at the top of the stack.
Key Properties of Stacks
- Order: Stack follows the LIFO principle for adding/removing/accessing stack elements.
- Access: Elements in the stack are accessible only from one end, the top.
- Restricted Operations: It allows only two primary operations, push to insert elements in the stack, and pop to remove elements from the stack.
- Applications: Stack is a proper data structure in applications where order of operations is critical.
What is the LIFO Principle?
- Push: Adds an element to the top of the stack.
- Pop: Removes the top element from the stack.
These two operations ensure that only the most recent data is accessible, making stacks ideal for scenarios where the order of operations is critical.
Real-World Analogy
To better understand a stack, imagine a pile of books in a library. Every time you add a book, it goes on top of the pile. If you want to remove a book, you can only take the one on top because the others are underneath it. This simple behavior mimics how a stack works in data structures, where the most recent element added is the first to be removed.
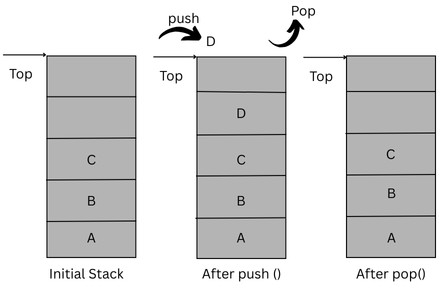
- The above figure shows an initial stack with three items, A, B, and C. The entry point for the stack is the Top of the stack.
- If you want to add an item D, you initiate a push operation and push the item D to the top of the stack. The resultant stack now consists of A, B, C, and D items with A at the bottom and D at the top.
- Now, if you want to remove an element from the stack, again you have to put it at the top of the stack. This is done using the pop operation. The pop operation removes the element at the top of the stack. In this case, it is D.
All stack operations are performed at the top of the stack and are the only manipulated entity.
In programming, stacks perform crucial tasks such as reversing sequences, temporarily holding data, and managing function calls in virtually every programming language.
Fundamental Stack Operations in DSA
The stack data structure, working on the LIFO principle, supports four primary actions: push, pop, peek, and checking whether it’s empty or full. These operations define how elements are added, accessed, and removed from the stack.
1. Push (Insertion)
The push operation adds an element to the top of the stack. If the stack has enough space, the new element pushed into the stack will appear on top of the last.
Example: If a stack contains [10, 20, 30] and you perform a push (40), the stack becomes [10, 20, 30, 40].
2. Pop (Deletion)
The pop operation removes the element from the top of the stack. As the stack follows the LIFO principle, only the last added element (i.e., the one at the top) can be removed. After the pop operation, the next element in the stack is the top element.
Example: If the stack is [10, 20, 30, 40], a call to pop () will remove the top element, 40, from the stack. The stack will then be [10, 20, 30], and element 40 will be returned.
3. Peek/Top
The peek (also called top) operation returns the value at the top of the stack without removing it from the stack. The peek operation is useful when you want to know what’s currently on top of the stack without modifying the structure.
Example: In a stack [10, 20, 30, 40], a peek () function call will return 40 without changing the stack.
4. isEmpty
The isEmpty stack operation checks whether the stack contains any elements. It returns true if the stack is empty and false if it has elements. The stack is always checked to see if it is empty before a pop or peek operation.
Example: If the stack is [], isEmpty will return true. If the stack is [1, 2, 3], isEmpty will return false.
5. isFull (in case of fixed-size stack)
This operation is relevant in the case of a bounded stack (one with a fixed size, such as an array-based stack); the isFull operation checks whether the stack has reached its maximum capacity. It helps in scenarios where the stack cannot grow dynamically. This function call is performed before inserting any value in the stack.
Example: If a stack has a size limit of 4 and is [1, 2, 3, 4], isFull will return true.
These basic stack operations form the backbone of the stack function, enabling efficient data management in LIFO order. These operations are fundamental to effective problem-solving in computer programming.
Stack Implementation
- Array-based Stack Implementation
- Linked List-based Stack Implementation
Array-based Implementation
In an array-based stack implementation, a fixed-size array stores stack elements. Each element occupies a specific index in the array, and a pointer called Top determines the current position of the last inserted element in the stack.
- Push Operation: When an element is pushed onto the stack, it is placed in the next available position in the array, and the top index is incremented by one.
- Pop Operation: To remove an element, the value at the top index is retrieved, and the top index is decremented.
- Peek Operation: The value at the top index is accessed without modifying the top.
Advantages of Array-based Stacks
- This is a simple and efficient method for small, fixed-size stacks.
- Arrays are contiguous blocks of memory, so there is a low memory overhead for the operations performed.
Limitations
- The stack size is fixed and must be known beforehand, which could lead to overflow (if the stack exceeds capacity) or underutilization of memory.
Pseudocode
stack[MAX]
top = -1
function push(x):
if top == MAX-1:
print("Overflow")
else:
top = top + 1
stack[top] = x
function pop():
if top == -1:
print("Underflow")
else:
top = top - 1
Linked List-based Stack Implementation
- Push Operation: A new node is created and inserted at the top when an element is pushed into the stack. The new node reference points to the previous top node, and the top is updated to this new node.
- Pop Operation: The top node is removed, and the top reference is updated to the next node in the list.
- Peek Operation: The element in the top node is accessed without removing the node.
Advantages of Linked List-based Stacks
- The stack size is dynamic, and there is no need to define an initial size.
- As long as memory is available, stack overflow is impossible.
Limitations
- A linked list-based stack implementation is more complex than an array-based stack.
- It requires extra memory for storing pointers, increasing memory overhead.
Pseudocode
struct Node {
int data;
Node* next;
}
top = NULL
function push(x):
newNode = createNode(x)
newNode->next = top
top = newNode
function pop():
if top == NULL:
print("Underflow")
else:
temp = top
top = top->next
delete(temp)
Time and Space Complexity
The following table shows the time and space complexities of stack operations for the array-based and linked list-based stack implementations:
| Operation | Array Implementation | Linked List Implementation |
|---|---|---|
| Push | O(1) | O(1) |
| Pop | O(1) | O(1) |
| Peek | O(1) | O(1) |
| isEmpty | O(1) | O(1) |
| Space | Fixed, O(n) | Dynamic, O(n + pointers) |
Applications of Stack in Programming
Stacks should not be considered mere theoretical concepts. They have practical applications across various fields in computer science and are incredibly versatile. Stacks’ ability to manage data with the LIFO principle makes them ideal for multiple tasks, from solving mathematical expressions to handling backtracking in complex algorithms. Here are some key applications of stacks.
1. Expression Evaluation
Stacks help convert infix expressions (e.g., A+B) to postfix (AB+) or prefix (+AB). They are essential for evaluating postfix and prefix expressions.
In postfix expression evaluation, operands are first pushed onto the stack, and when an operator is encountered, it is applied to the topmost elements. The result of the operation is then pushed onto the stack. This process is repeated until the entire expression is evaluated.
For example, consider the postfix expression, 3 4 + 2 * 7 /. The sequence of steps to evaluate this expression using stacks is as follows:
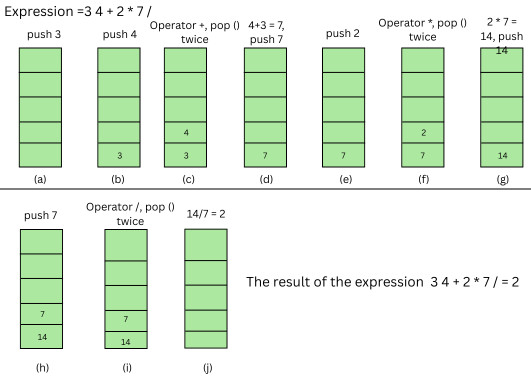
While infix expressions are more common, they can be challenging for machines to evaluate directly. However, postfix and prefix expressions are easier for computers to process and remove ambiguity.
2. Function Calls (Call Stack)
When a function calls another function, the return address and local variables are pushed onto the stack. This is the current state of the function. When the function completes execution and returns, all the variables saved are popped from the stack, effectively managing the execution flow.
3. Parentheses Matching
One of the most common uses of stacks is to check the balanced parentheses in code or mathematical expressions. Every opening parenthesis or bracket is verified for a corresponding closing parenthesis and correctly matched.
Each opening parenthesis is pushed onto the stack, and a stack is popped for each closing parenthesis. The expression is unbalanced if the stack is empty or mismatched at any point.
For the expression ((a + b) * (c – d)), the stack ensures that each opening parenthesis has a matching closing parenthesis.
4. Depth-First Search (DFS)
In graph traversal, DFS uses a stack (either explicit or implicit) to explore a graph by going as deep as possible along each branch before backtracking. When a stack is used implicitly, it is through recursion.
In DFS traversal for a graph, a stack keeps track of the nodes as they are visited. Once a node has no unvisited neighbors, the algorithm backtracks to the previous node on the stack.
5. Backtracking
Stacks are commonly used in backtracking algorithms, where decisions are made step-by-step. If a step leads to an incorrect solution, the algorithm can backtrack to a previous step. In backtracking, stacks store the state of each decision, and when a wrong path is detected, the program pops the last state off the stack to try another route.
The undo operation in applications like text editors is a typical example. Each action (typing, deleting, etc.) is pushed onto a stack. The last change is popped off the stack and reversed when you undo an action.
6. Recursive Algorithms
Almost all recursive algorithms rely on stacks to maintain their state across function calls. Recursion is implemented using an implicit stack, where each function call is pushed onto the stack until a base case is reached. After that, each call is popped off the stack as the function unwinds.
Advantages of Stacks
- Simplicity: Stacks are easy to implement using arrays or linked lists with simple push and pop operations that follow a straightforward LIFO principle.
- Efficiency: Stack operations, peek, push, and pop are fast and typically completed in O(1) time complexity.
- Memory Management: Stacks are memory efficient when implemented using arrays. They also have minimal overhead, needing only a pointer to the top.
- Recursion Support: Stacks are essential for managing recursive function calls and functions.
- Order Maintenance: Stacks are ideal for applications where the most recent element needs to be processed first.
- Locality of Reference: Performance is improved due to fast memory access in a stack structure.
Limitations of Stacks
- Limited Random Access: In a stack, only the top element is accessible, making it unsuitable for applications requiring access to other elements.
- Fixed Size (for arrays): Array-based stacks have a predefined capacity, leading to overflow or underutilization of memory.
- Potential for Overflow/Underflow: Mismanaging push and pop operations can cause errors.
- Not Scalable: Resizing dynamic stacks (e.g., linked lists) can be costly, while using arrays is not easy to scale.
- Recursive Limitations: Excessive recursion can lead to stack overflow, especially in deep recursive calls.
Stack Variations
- Double-Ended Stack (Deque-based): This type of stack allows insertion (push) and deletion (pop) operations at both the top and the bottom. This offers more flexibility than a standard stack.
- Two Stacks in an Array: Two stacks grow toward each other in the same array, ensuring the memory is used efficiently.
- Min/Max Stack: Performs push and pop operations while keeping track of the minimum or maximum in O(1).
- Multiple Stacks: When multiple independent stacks need to coexist, the multiple stacks are useful.
Stacks in Popular Programming Languages
Stacks can be efficiently implemented in almost all programming languages. In this section, we present the stack implementation in C++ and Python.
C++
#include <iostream>
using namespace std;
struct Node { //Node representing each item in the stack
int data;
Node* next;
Node(int val) : data(val), next(nullptr) {}
};
class LinkedListStack { //stack class
private:
Node* top;
public:
LinkedListStack() : top(nullptr) {}
~LinkedListStack() {
while (!isEmpty()) {
pop();
}
}
void push(int data) {
Node* newNode = new Node(data);
newNode->next = top;
top = newNode;
}
int pop() {
if (isEmpty()) {
cout << "Stack Underflow!" << endl;
return -1;
}
Node* temp = top;
int poppedVal = temp->data;
top = top->next;
delete temp;
return poppedVal;
}
int peek() {
if (isEmpty()) {
cout << "Stack is empty!" << endl;
return -1;
}
return top->data;
}
bool isEmpty() {
return top == nullptr;
}
void display() {
if (isEmpty()) {
cout << "Stack is empty.\n";
return;
}
cout << "Stack elements (top to bottom): ";
Node* current = top;
while (current != nullptr) {
cout << current->data << " ";
current = current->next;
}
cout << endl;
}
};
int main() {
LinkedListStack myStack; //create a stack object
myStack.push(10);
myStack.push(20);
myStack.push(30);
myStack.display();
cout << "Top element: " << myStack.peek() << endl;
myStack.pop();
cout << "Top element after pop: " << myStack.peek() << endl;
return 0;
}
Stack elements (top to bottom): 30 20 10 Top element: 30 Top element after pop: 20
Python
# Stack class with operations
class Stack:
def __init__(self):
self.stack = []
def push(self, element):
self.stack.append(element)
def pop(self):
if self.isEmpty():
return "Stack is empty"
return self.stack.pop()
def peek(self):
if self.isEmpty():
return "Stack is empty"
return self.stack[-1]
def isEmpty(self):
return len(self.stack) == 0
def size(self):
return len(self.stack)
# Create a stack
myStack = Stack()
myStack.push('a')
myStack.push('e')
myStack.push('i')
myStack.push('o')
myStack.push('u')
print("Initial Stack: ", myStack.stack)
print("Pop: ", myStack.pop())
print("Stack after Pop: ", myStack.stack)
print("Peek: ", myStack.peek())
print("isEmpty: ", myStack.isEmpty())
print("Stack Size: ", myStack.size())
Initial Stack: ['a', 'e', 'i', 'o', 'u'] Pop: u Stack after Pop: ['a', 'e', 'i', 'o'] Peek: o isEmpty: False Stack Size: 4
Conclusion
Stacks are the fundamental building blocks in computer science. The LIFO principle of stacks makes them invaluable in managing function calls, recursion, parsing expressions, and designing algorithms.
Stacks provide constant-time performance for push, pop, and peek operations regardless of whether they are implemented using arrays or linked lists. Stacks are everywhere, from compilers to operating systems, from text editors to web browsers, quietly ensuring efficiency and order.
By understanding and mastering stacks, developers strengthen their foundation in data structures and prepare for more advanced concepts like recursion, parsing, and algorithm design.
Related Reads:
- Why Learning Data Structures and Algorithms (DSA) is Essential for Developers
- Searching vs Sorting Algorithms: Key Differences, Types & Applications in DSA
- Arrays in Data Structures: A Complete Guide with Examples & Applications
- Data Structures and Algorithm Complexity: Complete Guide
- Tree in Data Structures: A Complete Guide with Types, Traversals & Applications
|
|
