Trie in Data Structures: A Complete Guide with Implementation & Applications

Ever wonder how suggestions appear the instant you begin typing into a search bar? It’s like the computer reads your mind. Behind that bit of magic, clever data structures are hiding, and the Trie is one of these silent heroes. In the realm of DSA (Data Structure and Algorithms), we have a number of approaches to manipulate, fetch, and preserve data efficiently. Trie is a great way to do this. It’s like a tree structure that offers an elegant solution for apps like a spell checker, autocomplete, or network routing table optimization.

What is a Trie?

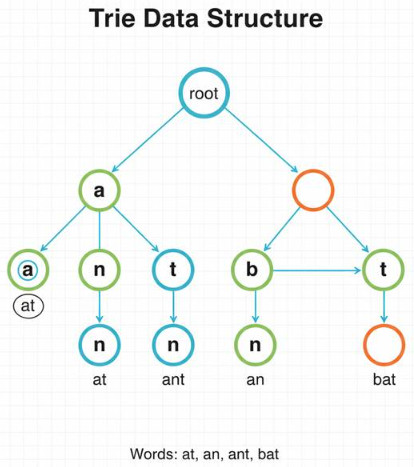
• Structure: A character is represented by each node in a trie. Usually working as a starting point, the root node does not store any characters. A node’s children indicate potential prefix continuations up to that node.
• Prefix Sharing: Reusing common prefixes is a trie’s main benefit. Cat, car, and can, for instance, only share the path c-a and branch at the third character. For big word sets with overlapping prefixes, this drastically reduces redundant storage.
• Word End Marker: To indicate whether the path from the root to that node corresponds to a complete word, nodes often have a Boolean flag (or counter). It would be impossible to discern between storing the word “bat” and just its prefix without this marker.

Although they are frequently referred to as prefix trees, tries can be expanded to handle sequences of symbols other than letters, including numbers, or even binary sequences in computer applications like IP routing.

Trie Implementation in DSA

Designing nodes and specifying operations like insertion, search, deletion, and prefix lookup are required steps in implementing a trie in DSA. Every node has:

Children’s Representation

• A fixed-size array, usually 26 for the lowercase English alphabet.
• A dictionary or hash map (for dynamic or larger alphabets, like Unicode).
• End-of-Word Flag: A node’s correspondence to the end of a valid string.

Detailed Core Operations

1. Insertion (word)
   • Start from the root.
     • For every character in the word:
     • Create the corresponding child node if it doesn’t already exist.
   • Move to the child node.
   • Mark the current node as a word-ending node after the last character.
   • Complexity: O(L), where L is the word’s length.
2. Search (word)
   • Go through the text after every character.
   • A word does not exist if any characters are missing from the text.
   • Validate whether the end-of-word flag is set at the final character.
   • Complexity: O(L).
3. Prefix Search (startsWith)
   • Similar to a search, it only verifies to see if the prefix path is present.
   • It is not necessary for the end-of-word flag to be true.
   • Complexity: O(P), where P is the prefix’s length.
4. Deletion (word)
   • More complicated than search or insertion.
   • Unmark the final character’s end-of-word flag.
   • Nodes can be reduced if they no longer form any other word (that is, they have no children or end nodes).
   • This ensures memory optimization without causing other stored words to break.

The size of the alphabet and the frequency of operations often decide a good implementation choice. For example, arrays are useful for a 26-letter English dictionary, but dictionaries or hash maps are necessary for a multilingual system to be flexible.

Trie vs Hash Table

Tries and hash tables are often compared when it comes to storing and searching strings because they are both efficient but customized for unique use cases.

Strengths of the Trie

1. Prefix Queries: Tries are perfect for autocomplete or dictionary-related tasks because they naturally support prefix searches.
2. Lexicographic Ordering: Without additional sorting, words saved in tries can be retrieved in alphabetical order.
3. Predictable Complexity: Regardless of dataset size, insert, search, and delete operations are always O(L).
4. No Hash Collisions: Attempts to avoid collision problems, in contrast to hash tables, which rely on hash functions.

Strengths of Hash Tables

1. Exact Word Lookup: With an average time complexity of O(1), hash tables are often faster for simpler membership checks.
2. Space Efficiency: Hash tables may utilize less memory for sparse datasets and those that have few overlapping prefixes.
3. Simplicity of Implementation: Particularly for inexperienced users, hash tables are easier to use and understand.

When to Use Each

• Use a trie when prefix-based queries are common, such as in search engines or autocompletion.
• Use a hash table when memory efficiency is critical and only precise searches are needed.

Applications of Trie in Programming

Tries have multiple uses in programming, especially in systems that depend heavily on text and search.

Autocomplete Engines

• The system can spontaneously recommend completion when a user inputs a prefix by navigating to the prefix node and searching through all of its descendants.
• IDEs, messaging apps, and search engines all make extensive use of tries.

Spell Checkers

• These applications try to store vast word dictionaries.
• By looking at neighboring nodes or prefixes, they can quickly establish whether a word exists and provide correction suggestions.

IP Routing

• Networking often uses longest prefix matching, and compressed tries, such as Patricia tries, efficiently store and match IP address prefixes.

Text Prediction and T9 Keyboards

• Numerical key sequences on old mobile devices were mapped to words.
• Stored in tries, it allowed for the retrieval of possible word matches from digit combinations.

Word Games

• Tries ensure that partial words are verified accurately during gameplay.
• Games like Scrabble or crossword solvers depend on fast word validation.

Search Suggestions and UX Systems

• In modern user interfaces, recommendations show up immediately after a user inputs.
• Even with large datasets, efforts are made to ensure that these recommendations are retrieved in microseconds.

Trie Data Structure with Examples

Let’s walk through a simple trie data structure with examples.

• Insert dog:
  • root → d → o → g (mark g as end).
• Insert dot:
  • root → d → o (shared) → t (mark t as end).
• Insert dove:
  • root → d → o → v → e (mark e as end).

• Search(dog) → true.
• Search(do) → false (unless explicitly stored as a word).
• PrefixSearch(do) → true.

This example shows how a trie effectively handles overlapping prefixes.

Advantages and Disadvantages of Tries

Advantages of Trie

• Effective Prefix Handling: When a system requires prefix lookups or completions, tries are the preferred choice.
• Deterministic Time Complexity: Word length, not dataset size, determines operations.
• Order Maintenance: To aid retrieval, data is kept in lexicographic order.
• No Collisions: Gets rid of issues with hash-based structures.
• Text System Scalability: Perfect for applications handling sizable text datasets, such as logs or dictionaries.

Disadvantages of Trie

• High Memory Usage: When utilizing arrays, nodes often have a large number of empty child pointers.
• Sparse Alphabets: Memory overhead increases sharply for large character sets (like Unicode).
• Complex Deletion: It is challenging to safely eliminate nodes without impacting shared paths.
• Overkill for Small Datasets: Binary search trees or hash sets are instances of simpler structures that may work better for smaller applications than tries.

Types of Trie (Compressed, Suffix, Radix)

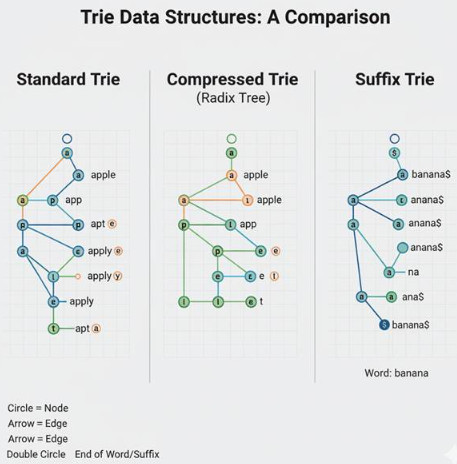
There are different kinds of trie to maximize performance and memory:

Standard Trie

• Every character is kept in a separate node.
• Easy, but it might take up a lot of space.

Compressed Trie (Radix Trie)

• Single-child node chains are compressed into single edges that hold substrings.
• Conserves space and depth.

Suffix Trie

• Stores all suffixes of a string.
• Advantageous for substring search issues.

Patricia Trie (Radix Trie)

• A space-efficient trie in which nodes that have a single child are combined.
• Extensively used by IP routing.
• Space and lookup speed are balanced differently in each variant.

Real-World Uses of Trie in Computing

1. Search Engines: Trie-based systems are used for autocomplete, instant search suggestions, and efficient indexing.
2. Compilers and Programming Tools: During parsing, identifiers, symbol tables, and reserved keywords are often kept in tries for faster access.
3. Database Indexing: Text indexing regularly uses tries to aid in the quick retrieval of keys with common prefixes.
4. Networking and IP Routing: Compressed tries, also called Patricia tries, help in swiftly matching IP addresses to routing tables.
5. File Systems: Directory paths naturally form trie-like structures, where each node represents a folder or file name.
6. Natural Language Processing (NLP): Language models, tokenization, and the efficient archiving of extensive lexicons are all applications of NLP.
7. Autocomplete in UX Design: To guarantee smooth user experiences, modern UI design makes use of autocomplete to decrease response times for dynamic search fields.

Trie for Developers: Code and Implementation Notes

When implementing a trie, developers and programmers must choose:

• Fixed-size array for restricted alphabets (e.g., 26 lowercase English letters).
• For bigger, sparser alphabets (Unicode), use a dictionary or hash map.

• For larger datasets, utilize compressed tries.
• Use the last deletion if memory isn’t important.

• Autocomplete engines.
• Frequency counters for words.
• Systems for processing text.

Implementing a trie in code is an ideal method for developers who want to sharpen their DSA skills.

Space Optimization Techniques in Tries

• Compressed Tries (Radix Trees): Build a single edge that stores a substring rather than a single character by collapsing chains of single-child nodes.
• Hybrid Child Representation: Use arrays for dense nodes and hash maps for sparse ones.
• Pointer Compression: Use compact representations, such as bitmaps or indices, rather than storing complete pointers for every child.
• Lazy Deletion: Designate nodes as unused and clean up later rather than deleting them all at once.

These methods allow experiments to be scaled for real-world datasets, like IP address lists or dictionaries.

Complexity Analysis of Trie Operations

• Insertion: O(L), where L = length of the word.
• Search: O(L).
• Prefix Search: O(P), where P = prefix length.
• Deletion: O(L), with additional cleanup overhead.
• Space Complexity: O(N x A), where N = total number of words and A = alphabet size (can be reduced via compression).

While tries ensure predictable performance independent of dataset size, space complexity is often the trade-off to consider.

Common Mistakes and Best Practices with Tries

1. Overlooking End-of-Word Flags: Without them, it is impossible to distinguish words from prefixes.
2. Using Arrays Blindly: Although arrays are rapid, they waste memory when dealing with large alphabets (like Unicode). When necessary, make use of maps.
3. Neglecting Deletion: Memory may become bloated if deletion is not done meticulously.
4. Not Considering Variants: In some cases, a suffix trie or compressed trie is better suited than a basic trie.
5. Overusing Tries: Streamlined data structures, such as hash tables, may be more efficient for small datasets or scenarios where only exact lookups are needed.

Developers can effectively balance memory and performance by satisfying these best practices.

Conclusion

With trie, developers can write systems such as spell checkers, autocompleters, or even new-age network tools with ease. Tries are a useful tool for optimization and something any developer should have in their toolbox when writing text-heavy apps.

This article demonstrates its applications in a variety of areas, such as compressed, suffix, and radix tries, and their practical use in computing. The trie is a base, which is nice to know, whether you are a student revising your DSA knowledge, a developer who works on production code, or just an enthusiast learning about data structures.

Additional Resources

• Data Structures and Algorithm Complexity: Complete Guide
• Why Learning Data Structures and Algorithms (DSA) is Essential for Developers
• Searching vs Sorting Algorithms: Key Differences, Types & Applications in DSA
• Tree in Data Structures: A Complete Guide with Types, Traversals & Applications
• Linked List in Data Structures: A Complete Guide with Types & Examples
• Arrays in Data Structures: A Complete Guide with Examples & Applications

Megana Natarajan