What Are Bitwise Algorithms in DSA?

When we first start learning programming, we generally think in terms of variables, loops, functions, and numbers. We hardly ever pause to consider the fact that everything is made of bits, or zeros and ones, and what’s actually going on underneath the hood.
Imagine being able to directly manipulate those bits, such as flipping, masking, moving, or cleverly combining them. That is the main objective of bitwise algorithms.
Bitwise algorithms are not restricted to compiler engineers or cryptography specialists, despite their intimidating sound. These are useful tools that can enhance the speed, efficiency, and even magic of your programs.
The world of bitwise operations, bitwise operators, and bit manipulation methods in Data Structures and Algorithms (DSA) will be explored in this article. In order for you to fully understand bitwise logic, not just the how, but also the why. We will keep the topic interesting by adding code snippets and making the connection. A Deep Dive into Bit Manipulation and Bitwise Operations for Everyday Programmers.
| Key Takeaways: |
|---|
|
What Are Bitwise Algorithms?
Basically, a bitwise algorithm is one that treats numbers as abstract quantities rather than treating them as such. It does this by directly manipulating the individual bits of binary data.
Within the computer, each integer is stored as a sequence of 0s and 1s, or in binary form. By working directly with these bits, bitwise algorithms perform calculations using bitwise operations.
For example, shifting bits to the left can accomplish the same thing as multiplying by 2 using standard arithmetic.
# Left shift example: multiply by 2 num = 5 # binary: 0101 result = num << 1 # shifts bits left -> 1010 (binary), equals 10 print(result) # Output: 10
That’s the magic of bitwise thinking; simple, low-level operations that do more than they seem.
Why Learn Bitwise Algorithms in DSA?
- Making use of bit manipulation techniques to optimize time complexity.
- Bitmasks are an efficient way to represent sets.
- Performing arithmetic faster.
- Identifying duplicate or unique numbers in arrays.
- Utilizing bit states to create ingenious Dynamic Programming solutions.
And the best part? Although many bitwise algorithms only need a few lines of code, they can drastically reduce execution time.
What are Bitwise Operations
Let us first define bitwise operations before diving into algorithms.
Bitwise operations act bit-by-bit on binary numbers. The most common ones are:
| Operator | Symbol | Description |
|---|---|---|
| AND | & | Returns 1 if both bits are 1 |
| OR | | | Returns 1 if either bit is 1 |
| XOR (Exclusive OR) | ^ | Returns 1 if exactly one of the bits is 1 |
| NOT | ~ | Flips the bits (0 → 1, 1 → 0) |
| Left Shift | << | Moves bits left (multiplies by powers of 2) |
| Right Shift | >> | Moves bits right (divides by powers of 2) |
Let’s see how they work.
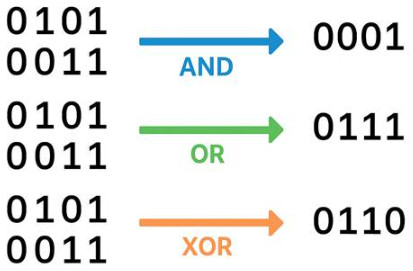
Example: Bitwise AND and OR
a = 5 # binary: 0101 b = 3 # binary: 0011 print(a & b) # AND -> 0001 = 1 print(a | b) # OR -> 0111 = 7
AND keeps only the bits that are 1 in both numbers.
OR combines all bits that are 1 in either number.
Bitwise Operators and Their Uses
The tools that allow us to carry out bitwise operations are called bitwise operators.
1. Determining if a number is off or even
We can check the final bit rather than using num % 2. The number is off if the last bit, or least significant bit, is 1.
num = 13
if num & 1:
print("Odd")
else:
print("Even")
Simple, fast, and elegant.
2. Set, Clear, and Toggle a Bit
These three operations are the basis of bit manipulation techniques.
| Operation | Code | Description |
|---|---|---|
| Set the n-th bit | num |= (1 << n) | Turns the nth bit ON |
| Clear the n-th bit | num &= ~(1 << n) | Turns the nth bit OFF |
| Toggle the n-th bit | num ^= (1 << n) | Flips the nth bit |
Example:
num = 5 # binary: 0101 # Set 1st bit num |= (1 << 1) # becomes 0111 (7) print(num) # 7
3. Counting Set Bits
Counting how many bits are 1 is a typical bitwise algorithmic problem.
Method 1: Using built-in function
bin(13).count('1') # Output: 3
Method 2: Using bitwise logic (Brian Kernighan’s Algorithm)
def count_bits(n):
count = 0
while n:
n &= (n - 1) # clears the lowest set bit
count += 1
return count
print(count_bits(13)) # Output: 3
Compared to verifying each bit separately, this is much faster.
Bit Manipulation Techniques in Practice
Bit manipulation is a way of thinking, not just a set of tricks.
1. Find the Only Non-Repeating Element
XOR all numbers together when all but one appear twice:
arr = [2, 3, 5, 4, 5, 3, 4]
unique = 0
for num in arr:
unique ^= num
print(unique) # Output: 2
Why is this efficient? XOR is commutative and associative since x ^ x = 0. There is only one unique number after all pairs cancel out.
2. Detect if a Number is a Power of 2
If a number is a power of 2, it has exactly one bit set.
def is_power_of_two(n):
return n > 0 and (n & (n - 1)) == 0
Example:
- 4 (100) → 4 & 3 = 0 → this is right
- 6 (110) → 6 & 5 = 100 != 0 → this is wrong.
3. Swapping Two Numbers Without a Temporary Variable
a, b = 10, 5 a ^= b b ^= a a ^= b print(a, b) # Output: 5, 10
Is it magic? Nope, it is just XOR logic.
4. Turning Off the Rightmost Set Bit
n = 12 # binary: 1100 n = n & (n - 1) # 1000 print(n) # 8
This is handy for counting bits or subset enumeration.
Bitwise Algorithms in Data Structures
Bitwise operations aren’t just mathematical tricks; they also show up in actual data structure issues.
Bitmask Representation of Sets
Bitmasks are often used in DSA to represent subsets.
Each element in the set {a, b, c, d} may represent a bit position. For example:
0001 → {d}1011 → {a, c, d}
By using integers as bitmasks, we can:
mask & (1 << i) to check membership.- Use
mask |= (1 << i)to add elements. - Use
mask &= ~(1 << i)to remove elements.
Dynamic programming on subsets, such as the prominent Traveling Salesman Problems (TSP) with bitmask DP, makes extensive use of it.
Using Bit Manipulation in Graph Algorithms
Bitmasks are an efficient way to define visited and unvisited nodes in certain graph issues, such as identifying subsets of nodes.
For example:
# Represent a path where nodes 0, 2, and 3 are visited visited = (1 << 0) | (1 << 2) | (1 << 3)
Using Bitwise Operations for State Compression
Exponential states are often seen in dynamic programming.
You can fit multiple Boolean flags into a single integer by using bitwise representation.
Example: Instead of an array [True, False, True, False], you can represent this as 0101 = 5.
This method drastically reduces space complexity and, at times, even accelerates runtime.
Advanced Bit Manipulation Techniques
You can examine more intricate patterns that rely on bit-level reasoning as you become more experienced and at ease.
Finding the Rightmost 1 Bit
n = 12 # 1100 mask = n & -n # isolates lowest set bit print(mask) # Output: 4 (0100)
Reversing Bits
def reverse_bits(n):
res = 0
for _ in range(32):
res = (res << 1) | (n & 1)
n >>= 1
return res
Bit reversal is a regular operation in image processing and cryptography tasks.
Bitwise vs Logical Operators
- Bitwise operators (&, |, ^) act on bits.
- Logical operators (and, or, not) act on Boolean values.
For example:
# Bitwise AND print(5 & 3) # 1 # Logical AND print(5 and 3) # 3 (since both are True-like values)
Real-World Use Cases of Bitwise Algorithms
There is way more to bitwise algorithms than meets the eye. Real systems that we use on a daily basis are fueled by them.
- Cryptography: The basis of encryption ciphers is bit shifts and XORs.
- Computer Graphics: Bit operations are utilized to manipulate color channels and pixels.
- Networking: Bitwise logic is a vital element of checksums, IP addressing, and subnet masks.
- Embedded Systems: Bitwise masks are leveraged to control hardware registers.
- Compression Algorithms: To conserve space, bits are packed closely together.
Thus, bitwise logic is working in the background the next time you use a VPN, view an image, or send data over Wi-Fi.
Advantages of Bitwise Algorithms
- Speed: Bitwise operations are carried out as fast as possible by the CPU in a single instruction.
- Memory Efficiency: Space is saved by using bits instead of larger data structures.
- Mathematical Elegance: A lot of bitwise techniques simplify complex operations to tidier one-liners.
- Control: You have more accurate control over your data when you work at the bit level.
Limitations and Pitfalls
- Readability: Freshers may find bitwise expressions confusing.
- Maintainability: It’s easy to forget the goal of a mask or shift in the absence of adequate documentation.
- Sign Issues: Signed and unsigned numbers behave differently when bit shifts are applied.
- Portability: Specific bit tricks, such as 32-bit integers, assume fixed bit widths.
As a typical rule, bit manipulation should only be used when it actually simplifies or optimizes, not only to impress.
Bitwise Thinking: The Mindset Shift
num & 1tells you if a number is odd.num & (num - 1)clears the lowest set bit.(num & -num)isolates the lowest set bit.(num | (num + 1))sets the rightmost 0 bit.
This shift in mindset can aid you in writing algorithms that are both elegant and efficient.
Common Interview Questions Related to Bitwise Algorithms
- Determine which element in an array is the only one that doesn’t repeat.
- Determine how many set bits there are in an integer.
- Understand whether a given number is a power of two.
- Determine where the rightmost set bit is located.
- Without using a third variable, swap two numbers.
- Use bitmasks to create every subset of a set.
Use bitwise addition instead of + or -.
You can assess your knowledge of binary logic by solving each of these using different bitwise algorithms.
Quick Reference Table
| Concept | Bitwise Trick | Purpose |
|---|---|---|
| Check even/odd | num & 1 | Last bit 0 = even |
| Set bit | num |= (1 << n) | Set the nth bit to 1 |
| Clear bit | num &= ~(1 << n) | Turn OFF the nth bit |
| Toggle bit | num ^= (1 << n) | Flip the nth bit |
| Check bit | (num & (1 << n)) != 0 | Is the nth bit ON? |
| Turn off the lowest set bit | num &= (num – 1) | Clear the lowest 1 |
| Isolate the lowest set bit | num & -num | Get the mask of the lowest 1 |
| Power of two check | num > 0 and (num & (num – 1)) == 0 | Exactly one bit set |
Bitwise Algorithms in Modern Computing
- Bit-level operations in machine learning make models lighter and faster. Time and energy are saved by replacing laborious floating-point computations with bitwise logic in methods such as quantization and binary neural networks.
- In competitive programming, bitmasks and bit manipulation techniques simplify intricate combinatorial problems, enhance dynamic programming states, and represent subsets while maintaining an elegant and efficient code.
- Bitwise control is also effective for embedded systems. Bigger operations cannot match the real-time precision that each bit offers by being able to read a hardware flag, turn on a motor, or toggle a sensor.
- Bitwise operations are critical even in data compression and security, whether it is packing data effectively or scrambling it securely through XORs and shifts.
- Bitwise algorithms subtly increase computing speed, efficiency, and intelligence in everything from artificial intelligence to embedded devices, demonstrating that bit-level programming remains one of the most powerful programming techniques.
Bitwise Algorithms: Small but Mighty
Similar to the unseen gears in a clock, bitwise algorithms are tiny, often disregarded, but required for efficient and smooth operation. They offer programmers with fine-grained control over data, enabling optimizations that lead to faster and leaner code. Understanding bitwise operations and bit manipulation techniques opens up a new dimension of problem-solving, whether you are working on cryptography, embedded systems, or just brushing up on your DSA skills.
Thus, don’t freak out the next time you observe code that includes odd-looking symbols such as &, |, or ^.
You’re just witnessing the ancient art of bitwise algorithms, the unsung heroes of modern computing.
Additional Resources
- Why Learning Data Structures and Algorithms (DSA) is Essential for Developers
- What is Code Optimization?
- Searching vs Sorting Algorithms: Key Differences, Types & Applications in DSA
|
|
