Linked List in Data Structures: A Complete Guide with Types & Examples

Shilpa Prabhudesai

In the data structures and algorithms (DSA) field, linked lists and arrays are among the most fundamental and widely used concepts. While arrays are often the go-to data structures for storing element sequences, they have limitations of fixed size and expensive insertion or deletion operations. This is where linked lists shine, and any computer science student, engineer, or data enthusiast finds it essential to master them.

Key Takeaways:
Linked lists are dynamic, provide flexibility in memory usage, and offer efficientinsertions and deletions. Like arrays, linked lists are also used to implement other data structures, such as stacks,queues, and dequeues. Linked lists are one of the fundamental building blocks in DSA, offering dynamic storage andefficient data manipulation. Understanding linked lists helps with mastering DSA and implementing efficient algorithms.

Key Takeaways:

Linked lists are dynamic, provide flexibility in memory usage, and offer efficientinsertions and deletions.
Like arrays, linked lists are also used to implement other data structures, such as stacks,queues, and dequeues.
Linked lists are one of the fundamental building blocks in DSA, offering dynamic storage andefficient data manipulation.
Understanding linked lists helps with mastering DSA and implementing efficient algorithms.

This is a complete guide to the linked list data structure, covering the basic concepts, types, applications, basic operations, advantages, and disadvantages of linked lists.

What is a Linked List in Data Structures?

A linked list is a list where elements called nodes are linked together. Each node contains data and a pointer pointing to the memory location where the next node is placed.

Unlike arrays, the elements in linked lists are not stored in contiguous memory locations. Nodes in linked lists are stored wherever there is free space in memory. Another benefit of linked lists is that the remaining nodes do not have to be shifted when adding or removing nodes. The order of nodes in linked lists is determined by these links and not their physical memory locations.

Key Components of Linked Lists

A linked list consists of the following key components:

Node: A linked list is a collection of one or more nodes. Each node consists of two parts:
- Data: The actual data or value stored in the node.
- Next: A pointer or reference pointing to the list’s next node.
Head: The head is a special pointer pointing to the linked list’s first node. It serves as the entry point for accessing the list. If the list is empty, the head pointer points to Null.

A typical linked list node is shown below:

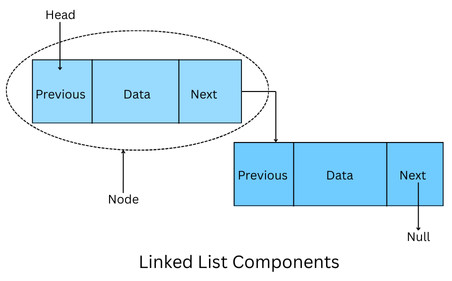
The node structure changes slightly depending on whether the linked list is singly or doubly linked. In a singly linked list, the node does not have a “previous” pointer but only “Data” and “Next.”

Nodes in a linked list are dynamically allocated and linked together using pointers. The last node in the list typically has its “next” pointer set to Null, indicating the end of the list.

Structure of a Linked List Node

A typical node can be defined in C or C++ as:

struct Node {
  int data;
  struct Node* next;
};

In Python, the linked list node is defined as:

class Node:
  def __init__(self, data):
    self.data = data
    self.next = None

A linked list contains one or more of these nodes. Each node holds data and a pointer or reference to the next node, forming a chain until the last node points to NULL or None in Python.

Types of Linked Lists in DSA

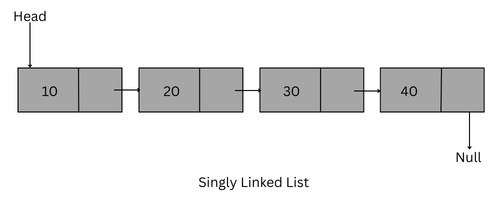
1. Singly Linked List

In a singly linked list, each node points to the next node in sequence, and the linked list can be traversed only in one direction. The last node points to NULL.

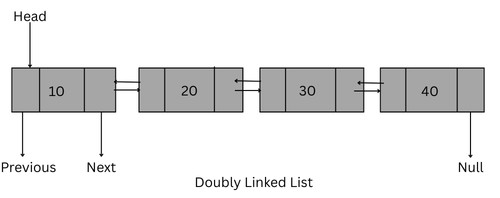
2. Doubly Linked List

In this type of list, each node contains two pointers or references. One reference points to the next node and another to the previous node.

With two references pointing to previous and next nodes, a doubly linked list can be traversed forward and backward.

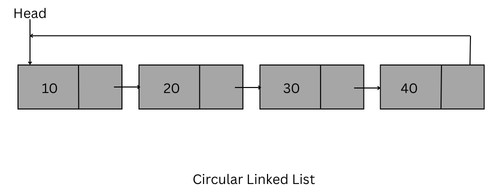
3. Circular Linked List

A circular linked list is a data structure in which the last node points back to the first node, forming a circular structure. It can be implemented using singly or doubly linked lists.

Basic Operations on Linked Lists

The basic operations that are performed on linked lists are as follows:

1. Traversal

A traversal operation involves visiting each node in the linked list sequentially to access or display elements. The traversal of elements starts from the head and then sequentially proceeds to the subsequent nodes, printing each node’s data.

The pseudocode for the traversal operation in a linked list is shown here:

def traverse(head):
  current = head
  while current:         //loop till last node
    print(current.data, end=" → ")
    current = current.next
  print("NULL")

The time complexity for linked list traversal is O(n), where n is the number of nodes in the linked list.

2. Insertion

Adding a node to the linked list is the insertion operation. Linked lists support the following types of insertions:

Insertion at the Beginning: A new node is added at the start of the list. The operation involved updating the head to point to a new node. The following sequence of steps is carried out for insertion at the beginning of the linked list:
1. Create a new node to be inserted.
2. Set its data to a given value.
3. Set its next pointer to the current head.
4. Update the head to point to the new node.
The pseudocode for this operation is:
```
def insert_at_beginning(self, data):
      new_node = Node(data)
      new_node.next = self.head
      self.head = new_node
    
```
The Time complexity of the insertion operation at the beginning of the linked list is O(1).
Insertion at the End: This operation requires traversing the list till the end and then adding a node. The steps performed for the insertion operation are:
1. Create a new node to be inserted.
2. Set its data to a given value.
3. Traverse the list until reaching the last node.
4. Set the last node’s next pointer to the new node.
The pseudocode for the insertion operation at the end of the list is:
```
def insert_at_end(self, data):
  new_node = Node(data)
  current = self.head
  while current.next:
    current = current.next
  current.next = new_node
```
The time complexity for insertion at the end is O(1) for doubly linked lists and O(n) for singly linked lists, as you need to traverse to the end of the list.
Insertion After a Given Node: This is the insertion operation in which a new node is added to the linked list at a specific position. The steps followed for this operation are:
1. Create a new node to insert.
2. Set its data to the given value.
3. Traverse the list until reaching the node before the desired position.
4. Adjust pointers to insert the new node.
The pseudocode for the insertion operation is:
```
def insert_at_position(self, position, data):
  new_node = Node(data)
  current = self.head
  for _ in range(position - 1):
    current = current.next
  new_node.next = current.next
  current.next = new_node
```
The time complexity for inserting a node at a specific position is O(n), as you need to traverse to the desired position.

3. Deletion

The deletion operation involves removing a node from a linked list and requires adjusting pointers so the chain remains intact. The deletion operation involves the following cases:

Deleting the Head Node: Removing the first node from the linked list involves only updating the head pointer. The sequence of steps is as follows:
1. Update the head to point to the second node.
2. Free the memory of the deleted node.
The pseudocode for this operation is:
```
def delete_at_beginning(self):
  if self.head:
    temp = self.head
    self.head = self.head.next
    del temp
```
The time complexity for deleting the head node in a linked list is O(1), as it only requires updating the head pointer.
Deleting a Node in the Middle: This method removes a node at a specific position in the linked list. The steps followed for deletion are:
1. Traverse the list until the node before the desired position is reached.
2. Adjust pointers to skip the node to be deleted.
3. Free its memory.
The pseudocode for this deletion operation is:
```
def delete_at_position(self, position):
  if position == 0:
    self.delete_at_beginning()
    return
  current = self.head
  for _ in range(position - 1):
    current = current.next
  temp = current.next
  current.next = temp.next
  del temp
```
The time complexity is O(n), as you need to traverse to the desired position, assuming you have a reference to the desired position. If the desired position is to be searched first, an additional O(n) traversal would be required, increasing the overall time complexity.
Deleting the Last Node: This operation removes the last node from the linked list. The steps performed for this operation are:
1. Traverse the list until the second last node in the list.
2. Update its next pointer to null.
3. Free the memory of the last node.
The pseudocode for the deletion of the last node is:
```
def delete_at_end(self):
  current = self.head
  if current:
    if not current.next:
      self.head = None
      return
    while current.next.next:
      current = current.next
    temp = current.next
    current.next = None
    del temp
```
The time complexity for deleting the last node is O(n) for singly linked lists, as you need to traverse to the second-last node, and O(1) for doubly linked lists.

4. Searching

The searching operation on a linked list is carried out by sequentially checking each node until the desired value is found. The pseudocode for this operation is:

def search(head, key):
  current = head
  while current:
    if current.data == key:
      return True
    current = current.next
  return False

The time complexity of the search operation on a linked list is O(n) in the average case.

5. Updating

This is a simple operation in which the new value is assigned to a specific node in place of the old one.

Complexity Analysis

The time complexity of operations on linked lists is generally better for insertion and deletion than for arrays, but worse for accessing elements by index or random access. The following table shows complexities for different operations in singly and doubly linked lists:

Operation	Singly Linked List	Doubly Linked List
Traversal	O(n)	O(n)
Insertion (begin)	O(1)	O(1)
Insertion (end)	O(n)	O(1)* (if tail kept)
Deletion (begin)	O(1)	O(1)
Deletion (end)	O(n)	O(1)* (if tail kept)
Searching	O(n)	O(n)

Linked List Implementation

C++:

The following program is the complete implementation of a linked list and its operations in C++:

#include <iostream>
using namespace std;

// Node structure for the linked list
struct Node {
  int data; // Data stored in the node
  Node* next; // Pointer to the next node

  // Constructor to initialize a new node
  Node(int val) : data(val), next(nullptr) {}
};

// LinkedList class
class LinkedList {
private:
  Node* head; // Pointer to the first node in the list

public:
  // Constructor to initialize an empty linked list
  LinkedList() : head(nullptr) {}

  // Linked list destructor
  ~LinkedList() {
    Node* current = head;
    while (current != nullptr) {
      Node* nextNode = current->next;
      delete current;
      current = nextNode;
    }
    head = nullptr; // Ensure head is null after deletion
  }

  // Insert a new node at the beginning of the list
  void insertAtBeginning(int data) {
    Node* newNode = new Node(data);
    newNode->next = head;
    head = newNode;
  }

  // Insert a new node at the end of the list
  void insertAtEnd(int data) {
    Node* newNode = new Node(data);
    if (head == nullptr) {
      head = newNode;
      return;
    }
    Node* current = head;
    while (current->next != nullptr) {
      current = current->next;
    }
    current->next = newNode;
  }

  // Delete the first node in the list (head)
  void deleteFromBeginning() {
    if (head == nullptr) {
      std::cout << "List is empty, nothing to delete." << std::endl;
      return;
    }
    Node* temp = head;
    head = head->next;
    delete temp;
  }

  // Delete a node with a specific value
  void deleteNode(int key) {
    if (head == nullptr) {
      cout << "List is empty, cannot delete." << endl;
      return;
    }

    // If the head node itself holds the key
    if (head->data == key) {
      Node* temp = head;
      head = head->next;
      delete temp;
      return;
    }

    Node* current = head;
    Node* prev = nullptr;

    while (current != nullptr && current->data != key) {
      prev = current;
      current = current->next;
    }

    // If the key was not found in the list
    if (current == nullptr) {
      cout << "Node with data " << key << " not found." << endl;
      return;
    }

    // Unlink the node from the list
    prev->next = current->next;
    delete current;
  }

  // display the list elements
  void display() {
    if (head == nullptr) {
      cout << "List is empty." << endl;
      return;
    }
    Node* current = head;
    while (current != nullptr) {
      cout << current->data << " -> ";
      current = current->next;
    }
    cout << "Null" << endl;
  }
};

int main() {
  LinkedList list;

  list.insertAtBeginning(10);
  list.insertAtEnd(20);
  list.insertAtBeginning(5);
  list.insertAtEnd(30);

  cout << "Initial list: ";
  list.display();

  list.deleteFromBeginning();
  cout << "List after element deleted from beginning: ";
  list.display();

  list.deleteNode(20);
  cout << "List after deleting node with value 20: ";
  list.display();

  list.deleteNode(100); // delete a non-existent node
  list.display();

  return 0;
}

The output of this program is:

Initial list: 5 -> 10 -> 20 -> 30 -> Null
List after element deleted from beginning: 10 -> 20 -> 30 -> Null
List after deleting node with value 20: 10 -> 30 -> Null
Node with data 100 not found.
10 -> 30 -> Null

Python:

Implementation and operations in a linked list using Python are shown in the program below:

class Node:
  def __init__(self, data):
    self.data = data
    self.next = None

def traverseAndPrint(head):
  currentNode = head
  while currentNode:
    print(currentNode.data, end=" -> ")
    currentNode = currentNode.next
  print("null")

def insertNodeAtPosition(head, newNode, position):
  if position == 1:
    newNode.next = head
    return newNode

  currentNode = head
  for _ in range(position - 2):
    if currentNode is None:
      break
    currentNode = currentNode.next

  newNode.next = currentNode.next
  currentNode.next = newNode
  return head

def deleteSpecificNode(head, nodeToDelete):
  if head == nodeToDelete:
    return head.next
  
  currentNode = head
  while currentNode.next and currentNode.next != nodeToDelete:
    currentNode = currentNode.next
  
  if currentNode.next is None:
    return head

  currentNode.next = currentNode.next.next

  return head

node1 = Node(7)
node2 = Node(3)
node3 = Node(2)
node4 = Node(9)

node1.next = node2
node2.next = node3
node3.next = node4

print("Original list:")
traverseAndPrint(node1)

# Insert a new node with value 97 at position 2
newNode = Node(97)
node1 = insertNodeAtPosition(node1, newNode, 2)

print("\nAfter insertion:")
traverseAndPrint(node1)

# Delete node4
node1 = deleteSpecificNode(node1, node4)

print("\nAfter deletion:")
traverseAndPrint(node1)

The output of this program is as follows:

Original list:
7 -> 3 -> 2 -> 9 -> null

After insertion:
7 -> 97 -> 3 -> 2 -> 9 -> null

After deletion:
7 -> 97 -> 3 -> 2 -> null

Advantages of Linked Lists

The linked list data structure has several advantages as follows:

Dynamic Memory Allocation: A dynamic linked list has no predefined size. They can grow or shrink in size as data is added or removed during runtime.
Efficient Insertions and Deletions: A linked list provides more efficient add-and-remove operations than arrays, as it only requires updating a few pointers and does not require shifting.
Versatility: Linked lists can implement advanced and complex data structures such as stacks, queues, trees, and graphs.
Memory Efficiency for Sparse Data: Linked lists are more memory-efficient than arrays if the number of elements is not known in advance or if the list is incomplete.

Disadvantages of Linked Lists

A linked list also has its own drawbacks, listed here:

Sequential Access: In a linked list, elements must be accessed sequentially from the start of the list. It is not possible to randomly access any element, like in arrays.
Increased Memory Overhead: Additional memory is needed to store a reference or a pointer to the next node, increasing the memory consumption.
Loss of Data Threat: If a pointer to the node is lost, all subsequent nodes of the linked list are inaccessible. This leads to data loss.
Complexity of Operations: Specialized operations, such as merging or reversing lists, can be more complex to implement than with arrays.

Applications of Linked Lists

Dynamic Memory Allocation: Linked lists are often used in dynamic memory allocation systems, in programming languages like C and C++, for efficient memory allocation. Memory blocks can be allocated/deallocated as needed using linked lists.
Implementation of Data Structures: Advanced data structures such as stacks, queues, hash chains, and adjacency lists in graphs can be implemented using linked lists.
Undo/Redo Functionality: Undo/Redo functionality in text editors is implemented using linked lists for history management. Each node in the linked list represents a state or action, allowing users to revert to previous states by traversing the list.
Polynomial Arithmetic: Polynomials can be represented using linked lists and also manipulated. Each node represents a term in the polynomial, with fields for the coefficient and exponent.
Music/Video Playlist Management: Backward/forward navigation in music applications can be efficiently done using linked lists. Here, each node represents a song, with fields for metadata such as title, singer, and duration. Users can maintain the playlist by adding, removing, or rearranging the songs.
Sparse Matrix Representation: Sparse matrices containing mostly zero values can be efficiently represented using linked lists, with each node representing a non-zero element along with its row and column indices.
Graphs: Linked lists can represent graphs, a collection of nodes (vertices) connected by edges. Each node in the linked list represents a vertex, and its adjacency list contains references to its connected vertices.
Symbol Tables: Compilers and interpreters use symbol tables that are represented using linked lists. Each node in the linked list contains information about a symbol, such as its name, type, and value.

Real-World Linked Lists Examples in Programming

Apart from applications discussed above, linked lists are also used in the day-to-day world in the following ways:

Web Browser History: When navigating through web pages online, you use browser buttons, such as back and forward. This implementation uses a doubly linked list. Each webpage visited is a node in the list, and the links (back and forward) ensure efficient traversal in both directions.
Operating System Task Scheduling: Operating systems can manage and schedule processes or tasks using linked lists. Each process is represented as a node, allowing the operating system to add, remove, and prioritize tasks efficiently.
Image Viewers: Like music players, image viewers use linked lists to navigate between images in a folder. Each image is a node, and the next and previous buttons allow users to view pictures sequentially.
Switching Between Applications (Alt+Tab/Command+Tab): Operating systems like Windows and macOS provide a feature to switch between open applications using keyboard shortcuts. This is often implemented using a circular linked list, ensuring seamless cycling through active applications.

Comparison: Linked List vs Array

Comparing linked lists with arrays is perhaps the easiest way to understand linked lists. Here is the table summarizing major differences between arrays and linked lists:

Feature	Arrays	Linked Lists
Memory	Elements are stored in a contiguous block of memory.	Elements (nodes) are stored in non-contiguous memory locations.
Memory allocation	Static	Dynamic
Size	Usually fixed-size, allocated at compile time.	Dynamic; memory is allocated for each node as it’s added.
Access	Fast random access using an index (O(1)).	Slow, requiring traversal from the beginning of the list (O(n)) to reach a specific element.
Insertions/Deletions	Slow, especially in the middle, as it requires shifting elements.	Fast, as only pointers need to be adjusted (O(1) if the location is known).
Memory Usage	Efficient for data, but can lead to wasted space if the array is oversized.	Less efficient for data due to the overhead of storing pointers in each node.

Linked List in Different Programming Languages

Various programming languages implement linked lists in different ways:

C: In the C language, linked lists are implemented using manual memory management with methods like malloc and free.
C++: The C++ language provides object-oriented design with classes that implement linked lists. The class std::list of the Standard Template Library (STL) provides a ready-to-use linked list implementation.
Java: It provides a built-in LinkedList class in the Java Collections Framework.
Python: There is no built-in linked list in Python, but lists behave like dynamic arrays. Linked lists can be implemented in Python manually.

Conclusion

Like arrays, linked lists are a cornerstone of computer science and programming. Through dynamic allocation, they provide the flexibility and efficiency required for dynamic applications that arrays cannot provide. While linked lists may not always be the optimal choice, especially in cases requiring random access, they form the basis for several advanced DSAs.

Mastering linked lists strengthens your understanding of pointers and memory management and also prepares you for real-world applications and technical interviews.